Matrix Factorization - LU Factorization

* 본 글은 선형대수학 복습을 상기시키기 위한 글로, 설명이 매우 부족할(?) 수 있습니다.

LU factorization

L: a unit lower triangular matirx

U: echelon form

Algorithm

LU factorizaiton을 수행하면 매우 간편하다.

LUx = b 연산에서, Ux를 y로 치환한다면,

Ly = b와 Ux = y의 방정식을 푸는 꼴이 된다.

 

알고리즘을 설명하면,

먼저 A를 elementary row operations을 통해서 echelon form으로 만들어준다. 이 form이 U가 된다.

그리고, elementary row operations을 수행하기 위해 곱해준 여러 E matrices를 inverse를 취하면 L이 된다.

 

밑에 예제를 보면 더욱 이해가 편하다.

Example

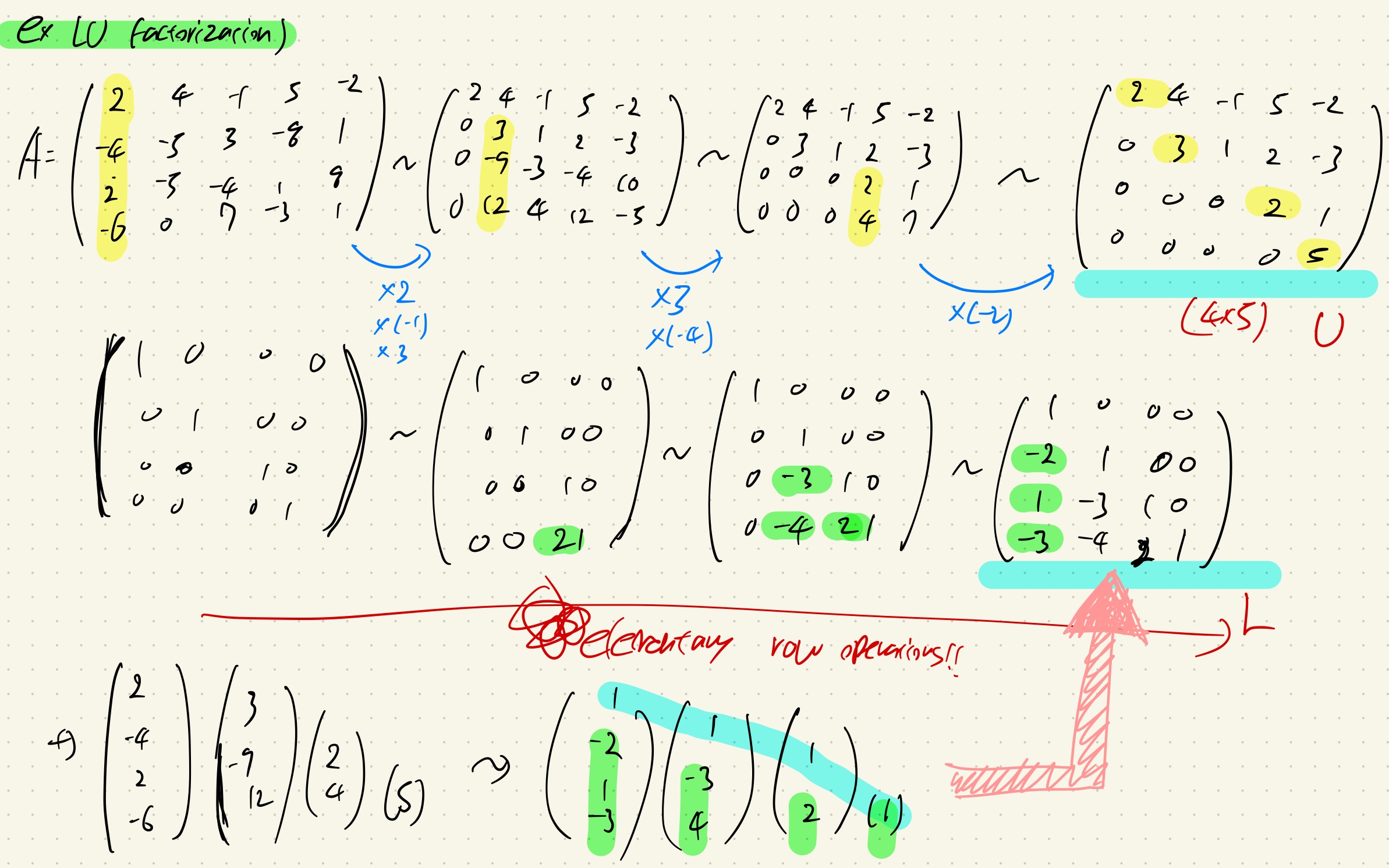
Elementary row operations이 편한 이유는, 전 글에도 언급되어 있지만,

inverse matrix를 구하기 매우 간편하고, 또한 연산도 매우 간편하다.

그래서 쉽게 L matrix를 계산할 수 있다!!!

row exchange

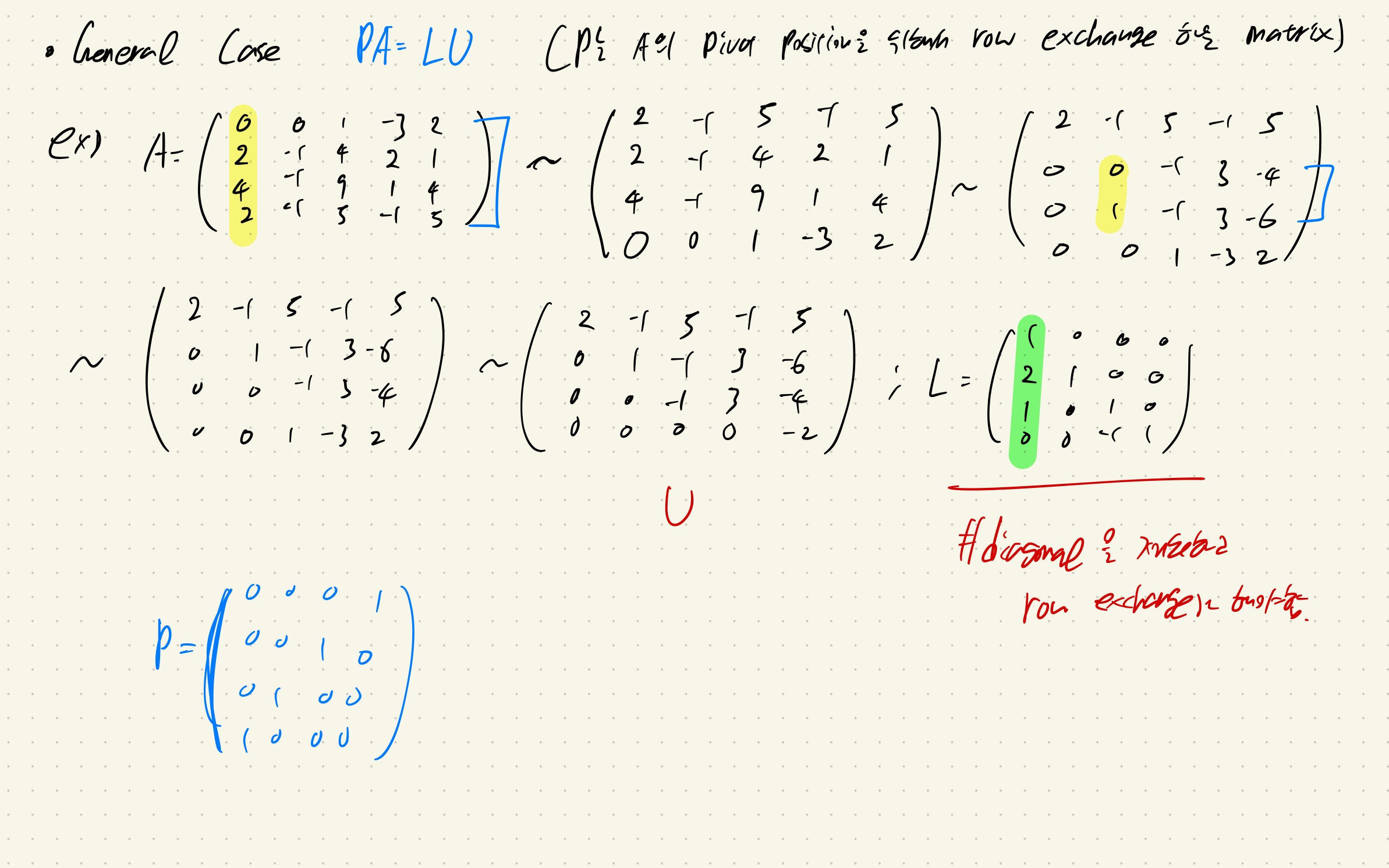
만약 echelon form을 만들기 위해서 행의 위치를 변경했다면, L에서도 변경해줘야 한다.

(단, diagonal elements은 제외하고)

LU factorization이 좋은 이유를 알려주는 것인데,

Ax = b의 해를 구하기 위해서 우리는 흔히 x = A^-1b를 수행한다.

 

여기서 A의 inverse를 손쉽게 구하면 좋지만, 만약 A가 sparse한 형태라면, A의 inverse는 매우 복잡하게 나온다.

그러나 L과 U는 A처럼 sparse한 형태로 나오기 때문에, 

이러한 경우에서 LU Factorization이 효과를 보여준다.