*Gaussian Splatting에 대한 간단한 논문 리뷰 입니다!
*이해를 돕기 위해 수식은 거의 제외했습니다.
GS 논문: repo-sam.inria.fr/fungraph/3d-gaussian-splatting/3d_gaussian_splatting_high.pdf
GS github: 3D Gaussian Splatting for Real-Time Radiance Field Rendering (inria.fr)
3D Gaussian Splatting for Real-Time Radiance Field Rendering
[Müller 2022] Müller, T., Evans, A., Schied, C. and Keller, A., 2022. Instant neural graphics primitives with a multiresolution hash encoding [Hedman 2018] Hedman, P., Philip, J., Price, T., Frahm, J.M., Drettakis, G. and Brostow, G., 2018. Deep blending
repo-sam.inria.fr
Introduction
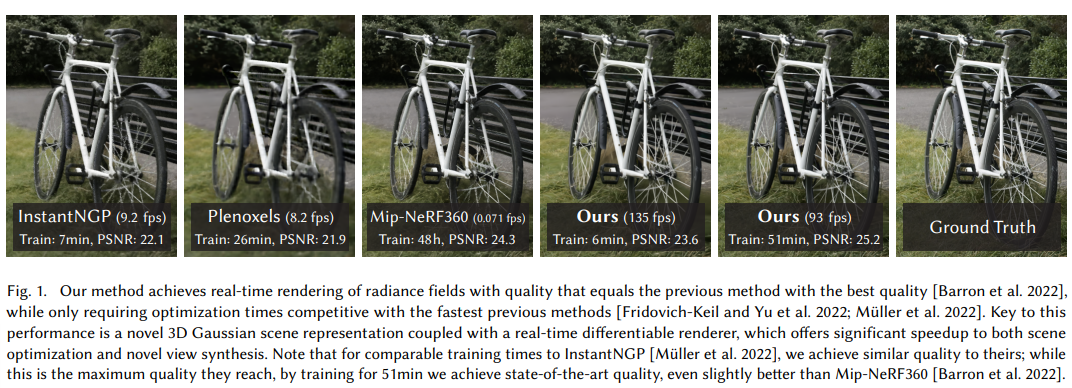
Gaussian Splatting(GS)은 Instant-NeRF보다 빠른 training time과 높은 성능을 보이는 모델로 큰 각광을 받고 있다.
GS는 3D gaussian distribution으로 image를 구성하게 되는데 되게 방법론이 특이하다.
과연 3D gaussian을 통해서 이미지의 color와 object를 어떻게 표현할 수 있는지 간단히 모델의 이론에 대해 살펴보자!
Method

3D-GS의 구조입니다!
3D-GS model structure를 보면 생소한 표현들이 있는데, 하나하나씩 살펴보고 가보겠습니다.
우선, 3D-GS의 구조는 다음과 같습니다.
1. SfM Points 생성 (NeRF에서 colmap을 통해서 생성되는 여러 카메라 파라미터들이 있었습니다.)
- Camera pose 및 Point cloud 정보를 SfM 알고리즘 통해서 얻고, 3D gaussian 초깃값으로 활용.
2. 생성된 3D gaussian과 camera pose를 활용해서 image plane에 2D gaussian으로 projection 합니다.
3. 미분가능한 tile rasterizer를 활용해서 2D gaussian을 image로 만듭니다.
4. Adaptive Density Control을 통해서 gaussian의 형태를 수정(변화) 합니다.
모델의 flow를 구체적으로 이해하기 위해, 논문에 소개된 algorithm code를 살펴보겠습니다.


첫번째 Algorithm1 코드에서 보여주고 있는 부분은, SfM과 initialization입니다.
1. SfM을 통해서 이미지의 point cloud를 추출합니다.
2. 그리고, S(covariances), C(colors), A(opacity)에 대한 learnable parameters를 지정합니다.
- 추가로, color에 대한 값은 SH-coefficients을 활용하게 됩니다.
위에서 initialization 된 값으로 3D gaussian을 생성하게 되는데, SfM에서 생성된 각 point 별로 3D gaussian을 갖게 됩니다.
이때 우리는 3D gaussian에 대해서 다음과 같이 생각해 볼 수 있습니다..!
3D-GS의 목적은 각 point 별로 생성된 3D gaussian 분포를 통해서 image를 생성하는 것이다. 그렇다면 모델 학습을 통해서 3D gaussian의 분포를 학습하면 되겠구나!
== 그러면, gaussian이 가지는 모수를 예측하도록 모델을 설계하면 되겠다!

# https://github.com/graphdeco-inria/gaussian-splatting/tree/b2ada78a779ba0455dfdc2b718bdf1726b05a1b6
# Point Cloud
self._xyz = nn.Parameter(fused_point_cloud.requires_grad_(True))
# SH(spherical harmonics) 계수
self._features_dc = nn.Parameter(features[:,:,0:1].transpose(1, 2).contiguous().requires_grad_(True))
self._features_rest = nn.Parameter(features[:,:,1:].transpose(1, 2).contiguous().requires_grad_(True))
# 3D gaussian
self._scaling = nn.Parameter(scales.requires_grad_(True))
self._rotation = nn.Parameter(rots.requires_grad_(True))
# A matrix
self._opacity = nn.Parameter(opacities.requires_grad_(True))따라서 gaussian의 분포가 변화(transformation)되는 것은 임의의 scaling matrix S와 rotation matrix R이 영향을 주는 것이라고 생각할 수 있습니다.
그렇기 때문에, 3D-GS는 S와 R에 대한 matrxi를 parameters로 설정하여 learnable하도록 합니다!
또한 point cloud에 대한 xyz도 모델이 학습할 때마다 위치를 잘 반영할 수 있도록(?) learnable하게 학습합니다!
따라서, 3D gaussian의 평균과 공분산이 3D-GS에서 가장 중요한 parameters이다!
(+ 평균의 초깃값은 point cloud 값)

두번째 부분은, tile rasterize와 backpropagation에 대한 부분이다..!
Rasterize 함수를 보면, point cloud(M), covariances(S), colors(C), opacity(A), camera pose(V)가 입력값으로 활용된다! Tile Rasterization에 대해서 좋은 설명들이 있어서 아래에 리스트업을 했다!
[Rasterize 쉬운 이해]
[Rasterize 상세 알고리즘 리뷰]
Tile Rasterizaiton을 간단하게 요약하면 다음과 같이 표현할 수 있다!
(3D-GS 기준)
1. 16x16 pixel 사이즈를 가지는 tile을 정의합니다.
2. 3D gaussian을 image plane에 2D projection을 수행한다.
3. 각 tile 내에 겹친 gaussian이 있다면, depth를 기준으로 정렬한다.
4. Depth를 기준으로 정렬된 gaussian을 순차적으로 고려해서, opacity, color 등등을 accumulate해서 해당 point의 RGB값을 rendering 합니다. (NeRF 개념)
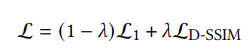
Tile Rasterization을 수행하고 난 뒤, 나온 image를 가지고 loss function을 계산한다.
신기하게도, NeRF와 다르게 L1 loss를 활용한다.
기타자료
Spherical Harmonics
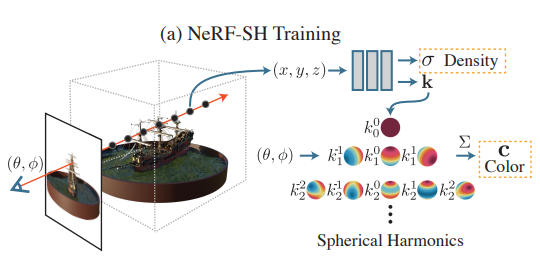
+) SH는 구면조화함수의 줄임말로 구(sphere)에서 정의되는 방위각, 고도각에 따라서 구 표면에 대한 물리적 특성을 해석하는 함수를 의미합니다!
+) SH-encoding이나 SH-function을 활용해서 colors를 예측하는데 활용하는 여러 논문 사례가 있습니다!
+) Plenoxels, Plenoctrees 등등 논문 참고
Tile Rasterization algorithm code

+) ScreenspaceGaussians를 통해서 2D gaussian으로 projection 된다.
+) 마지막에 있는 BlendInOrder 함수를 통해서 각 gaussian의 opacity color values를 활용해 rendering을 수행하는 것 같다.

+) 3D gaussian이 2D gaussian으로 projection될 때 공분산 수식
+) 제대로 이해하지는 못했는데, 나중에 필요하면 다시 이해..ㅎㅎ
References
[논문 리뷰] 3D Gaussian Splatting (SIGGRAPH 2023) : 랜더링 속도/퀄리티 개선 (tistory.com)
[논문리뷰] 3D Gaussian Splatting — 정리용 블로그 (tistory.com)
2024.05.04 kyujinpy 작성.



