*Mamba 논문 리뷰 시리즈1 입니다! 궁금하신 점은 댓글로 남겨주세요!
시리즈 1: Hippo
시리즈 2: LSSL
시리즈 3: S4
시리즈 4: Mamba
시리즈 5: Vision Mamba
HiPPO paper: https://arxiv.org/abs/2008.07669
HiPPO: Recurrent Memory with Optimal Polynomial Projections
A central problem in learning from sequential data is representing cumulative history in an incremental fashion as more data is processed. We introduce a general framework (HiPPO) for the online compression of continuous signals and discrete time series by
arxiv.org
HiPPO github: https://github.com/HazyResearch/hippo-code
GitHub - HazyResearch/hippo-code
Contribute to HazyResearch/hippo-code development by creating an account on GitHub.
github.com
Contents
- High-order Polynomial Projection Operators
- General HiPPO Framework
- High Order Projection: Measure Families and HiPPO ODEs
- HiPPO-LegS: Scaled Measures for Timescale Robustness
- HiPPO & State-Space Model
4. Furthermore: LSSL
Simple Introduction

Transformer가 서서히 왕좌의 자리의 빼앗기고 있다(?)
그것은 바로, 차세대 아키텍쳐, mamba가 등장했기 때문이다!
Mamba의 기본적인 아이디어는, SSM (state-space model)를 기반으로 만들어졌는데,
SSM을 활용한 딥러닝의 시초(?)인 HiPPO를 먼저 간단하게 이해해보자!
그리고 차근차근 논문 step을 밟아가면서, mamba를 알아보자!
Method
High-order Polynomial Projection Operators

논문에서는 Problem Setup을 잘 봐야한다!
- time-series function f(t)를 정의하자!
- 이때, f(t)에 매핑되는 space는 일단 기본적으로 다루기 힘들 정도로 클 것이다!
- 그리고, 모든 time (history)에 대해서 기억하지 못한다.
- HiPPO 논문에서는, 적절한 subspace에 f(t)를 approximation하는 문제를 해결하고자 한다!
General HiPPO Framework

논문에서는, 사실 이해하기가 조금 어렵게 설명되어 있다. (수식이 많아서...)
따라서, framework 사진을 보면서 직관적으로 HiPPO의 개념을 이해해보자!
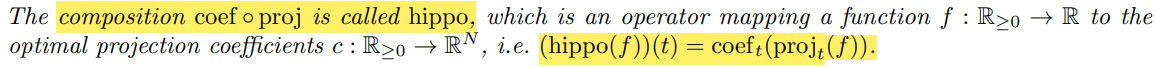
[HiPPO Framework]
(1) Time에 따라 변하는 함수 f를 정의.
(2) 각 시간 t0, t1 , ... T에 따라 optimal하게 projection되는 polynomial function g(t)가 존재.
-> g(t)를 정의하는 방법은 뒷부분에서 설명. (measures u(t)에 따라 결정됨.)
(3) g(t)를 R^N space vector를 가지는 coef.로 mapping.
-> (2) + (3)을 합쳐서 HiPPO 라고 부름.
(4) 시간 변화율에 따른 continous-time HiPPO ODE(ordinary dynamic equation) 정의.
-> HiPPO ODE에서 f는 t시점까지의 f 함수.
(5) 하지만, 우리가 다루는 공간은 이산적이므로, 이를 회귀 (recurrence)문제로 다시 정의.
-> [k+1번째의 Coef.] = [고정된 A, B, f & k번째 Coef.]의 matrix 곱셈 연산으로 이루어짐.
*위의 HiPPO framework는 uniform measures를 활용함.
여기까지는, 시간 함수 f(t)를 projection시키고, coeff로 매핑해서 c(t)를 찾는게 HiPPO의 framwork이라고 이해하셨다면 완벽합니다!
(아래 부분에서, measure와 모델의 학습 방법, 그리고 HiPPO와 SSM간의 관계에 대해 좀 더 자세히 설명하도록 하겠습니다!)
High Order Projection: Measure Families and HiPPO ODEs
논문의 저자들은, projection matrix를 결정지을 measures에 대해서 기본적인 2가지 transition을 보여주고 있습니다!
1. translated Legendre (LegT)
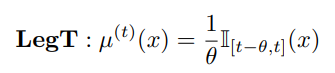

2. translated Laguerre (LagT)
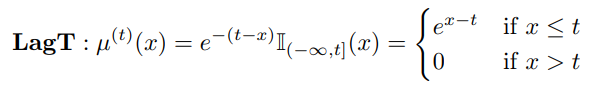
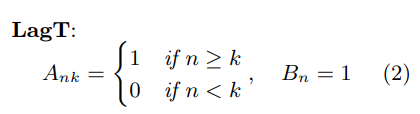
위의 measure를 통해서 continuous한 g(t)를 어떻게 구성하는지 아래의 코드에서 살펴볼 수 있습니다!
# HiPPO matrices
# https://github.com/state-spaces/s4/blob/e757cef57d89e448c413de7325ed5601aceaac13/src/models/hippo/visualizations.py#L38
def transition(measure, N, **measure_args):
# Laguerre (translated)
if measure == 'lagt':
b = measure_args.get('beta', 1.0)
A = np.eye(N) / 2 - np.tril(np.ones((N, N)))
B = b * np.ones((N, 1))
# Legendre (translated)
elif measure == 'legt':
Q = np.arange(N, dtype=np.float64)
R = (2*Q + 1) ** .5
j, i = np.meshgrid(Q, Q)
A = R[:, None] * np.where(i < j, (-1.)**(i-j), 1) * R[None, :]
B = R[:, None]
A = -A
(...생략...)
return A, B여기서 중요한 포인트는, continuous한 g(t)를 구성하는 matrix는 A와 B라는 사실 입니다!
(HiPPO framework: A * C + B * f)
HiPPO-LegS: Scaled Measures for Timescale Robustness
위의 measures에서 더 memory적으로 효율적으로 tight하게 approximation이 가능한
scaled Legendre measure (LegS)를 논문의 저자들은 제안하고 있습니다. (사실 이게 main measures!)
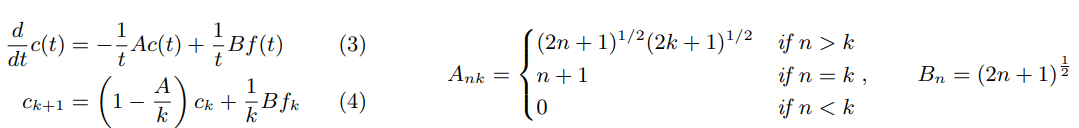
def transition(measure, N, **measure_args):
(...생략...)
# Legendre (scaled)
elif measure == 'legs':
q = np.arange(N, dtype=np.float64)
col, row = np.meshgrid(q, q)
r = 2 * q + 1
M = -(np.where(row >= col, r, 0) - np.diag(q))
T = np.sqrt(np.diag(2 * q + 1))
A = T @ M @ np.linalg.inv(T)
B = np.diag(T)[:, None]
B = B.copy() # Otherwise "UserWarning: given NumPY array is not writeable..." after torch.as_tensor(B)
(...생략...)
return A, B위와 같이 LegS로 A, B matrix를 정의할 수 있습니다!
HiPPO & State-Space Model


State-Space Model의 기본 motivation은 위와 같은 dynamic linear system을 해결하는 것이다!
쉽게 얘기하면, time-series를 떠올릴 수 있는데 여기서의 큰 특징은 X_t+1 = A * X_t + B * u_t라는 것이다!
즉, 각 시간 t에 따른 output value를 결정하는 X_t가 이전의 X_t-1에 영향을 받는다는 것이다.
아래의 코드를 보면서, HiPPO와 한번 연결지어보자!
# https://github.com/state-spaces/s4/blob/main/src/models/hippo/visualizations.py
class HiPPO(nn.Module):
"""Linear time invariant x' = Ax + Bu."""
def __init__(self, N, method='legt', dt=1.0, T=1.0, discretization='bilinear', scale=False, c=0.0):
"""
N: the order of the HiPPO projection
dt: discretization step size - should be roughly inverse to the length of the sequence
"""
super().__init__()
self.method = method
self.N = N
self.dt = dt
self.T = T
self.c = c
A, B = transition(method, N)
A = A + np.eye(N)*c
self.A = A
self.B = B.squeeze(-1)
self.measure_fn = measure(method)
C = np.ones((1, N))
D = np.zeros((1,))
dA, dB, _, _, _ = signal.cont2discrete((A, B, C, D), dt=dt, method=discretization)
dB = dB.squeeze(-1)
self.register_buffer('dA', torch.Tensor(dA)) # (N, N)
self.register_buffer('dB', torch.Tensor(dB)) # (N,)
self.vals = np.arange(0.0, T, dt)
self.eval_matrix = basis(self.method, self.N, self.vals, c=self.c) # (T/dt, N)
self.measure = measure(self.method)(self.vals)
def forward(self, inputs, fast=True):
"""
inputs : (length, ...)
output : (length, ..., N) where N is the order of the HiPPO projection
"""
inputs = inputs.unsqueeze(-1)
u = inputs * self.dB # (length, ..., N)
if fast:
dA = repeat(self.dA, 'm n -> l m n', l=u.size(0))
return unroll.variable_unroll_matrix(dA, u)
c = torch.zeros(u.shape[1:]).to(inputs)
cs = []
for f in inputs:
c = F.linear(c, self.dA) + self.dB * f
cs.append(c)
return torch.stack(cs, dim=0)(1) method를 통해서 measures 정의. (transition 함수)
(2) HiPPO __init__ 함수를 통해서, continous한 g(t)를 구성하는 A와 B matrix 정의.
(3) State Space Model (SSM) 정의를 위한 C와 D를 각각 1과 0으로 설정.
(4) 현재 continuous function이므로, 이를 discrete하게 만들어주기 위해 signal.cont2discrete 적용.
(5) 최종적인 Discrete HiPPO ODE에 활용되는 Ak, Bk를 정의. (코드상에는 dA와 dB)
(6) forward 함수를 통해서, coeff를 계산.
-> inputs은 time series 함수 f(t)에 해당.
-> dA * Ck + dB * f를 통해서 Ck+1을 예측.
*해당 equations을 통해서, k시점의 값을 예측할 수 있음.
Result
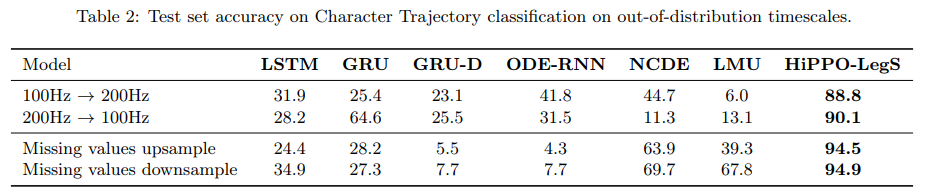
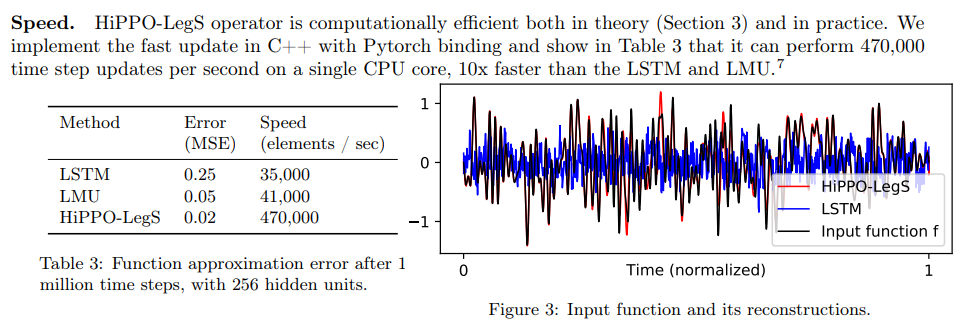
- 속도와 성능적인 측면에서 모두 강점을 가지고 있다.

- HiPPO framework에서 활용되는 measures에 따른 f(t) projection 시각화 결과이다!
Furthermore
LSSL 논문 리뷰: https://kyujinpy.tistory.com/147
[Mamba 논문 리뷰 2] - LSSL: Combining Recurrent, Convolutional, and Continuous-time Models with Linear State-Space Layers
*Mamba 논문 리뷰 시리즈1 입니다! 궁금하신 점은 댓글로 남겨주세요!시리즈 1: Hippo시리즈 2: LSSL시리즈 3: S4시리즈 4: Mamba시리즈 5: Vision MambaLSSL paper: [2110.13985] Combining Recurrent, Convolutional, and Continuou
kyujinpy.tistory.com
- Mamba 논문리뷰 2번째 시리즈 입니다!
- HiPPO보다 간단한데 직관적이여서 추천드립니다!
- 2024.06.26 Kyujinpy 작성.
*광고 수익은 연말에 기부를 할 생각입니다! 봐주신 여러분 감사드립니다 ㅎㅎ



