*Mamba 논문 리뷰 시리즈3 입니다! 궁금하신 점은 댓글로 남겨주세요!
시리즈 1: Hippo
시리즈 2: LSSL
시리즈 3: S4
시리즈 4: Mamba
시리즈 5: Vision Mamba
S4 paper: [2111.00396] Efficiently Modeling Long Sequences with Structured State Spaces (arxiv.org)
Efficiently Modeling Long Sequences with Structured State Spaces
A central goal of sequence modeling is designing a single principled model that can address sequence data across a range of modalities and tasks, particularly on long-range dependencies. Although conventional models including RNNs, CNNs, and Transformers h
arxiv.org
S4 github: Efficiently Modeling Long Sequences with Structured State Spaces | Papers With Code
Papers with Code - Efficiently Modeling Long Sequences with Structured State Spaces
#2 best model for Sequential Image Classification on Sequential CIFAR-10 (Unpermuted Accuracy metric)
paperswithcode.com
Contents
5. Furthermore
Simple Introduction

시계열이나 sequence modeling에서 LRD (long-range dependencies)를 handling하는 것은 매우 중요한 작업이다.
최근에는 기존의 시계열 모델들 CTM(continuous-time model), RNN, CNN 대신 SSM (state-space model)이 떠오르고 있다.
앞서서 우리는 HiPPO와 LSSL을 통해서 SSM과 SSM을 deep learning에 적용하는 방법에 대해서 살펴봤다.
LSSL은 HiPPO보다 뛰어났지만, 실질적으로 메모리나 계산적인 측면에서 활용되기 어렵다는 단점이 있었다.
S4는 LSSL의 이러한 단점을 보완한 SSM이다!
과연 어떻게 해결했는지 살펴보자!
Background Knowledge: LSSL
LSSL 논문 리뷰: https://kyujinpy.tistory.com/147
[Mamba 논문 리뷰 2] - LSSL: Combining Recurrent, Convolutional, and Continuous-time Models with Linear State-Space Layers
*Mamba 논문 리뷰 시리즈1 입니다! 궁금하신 점은 댓글로 남겨주세요!시리즈 1: Hippo시리즈 2: LSSL시리즈 3: S4시리즈 4: Mamba시리즈 5: Vision MambaLSSL paper: [2110.13985] Combining Recurrent, Convolutional, and Continuou
kyujinpy.tistory.com
- Mamba 논문 리뷰 두번째 시리즈인 LSSL 입니다!
Method

S4 논문에서는 지금까지의 모든 SSM 관점에 대해서 효율적으로 연산하는 방법을 제안하고 있다.
1. Continous representation (HiPPO)
2. Recurrent representation (LSSL)
3. Convolutional representation (LSSL)
Motivation: Diagonalization

Discrete-time SSM (recurrent SSM)에서 computational cost의 주 요인은 A matrix의 반복된 곱셈 연산이다.
따라서 이 문제를 해결하기 위해, A, B, C matrix를 conjugate하는 관점으로 바라본다.
위의 diagonalization을 통해서 time-complexity가 O(N^2L)에서 O(NL)까지 줄어드는 것을 확인할 수 있다!
(*D가 생략된 이유는, 단순한 잔차 연결이기 때문에 계산의 간편성을 위해서 제외함.)

그러나 diagonalization을 통해서 A, B, C를 conjugate하는 방법은 아쉽게도 HiPPO matrix에서 numerical issue로 계산이 안 될 수 있다고 논문의 저자들은 말하고 있습니다.
*(정확한 이해는 못함 ㅠ; Appendix B의 증명 참고...)
이러한 문제를 해결하기 위해 논문의 저자들은 NPLR (Normal Plus Low-Rank) 방법론을 제시했습니다.
Normal Plus Low-Rank (NPLR)

NPLR은 A matrix를 아래의 matrices로 분해할 수 있다는 것을 의미합니다!
- unitary matrix V
*unitary matrix: 복소수 정사각 행렬이고, V matrix의 conjugate transpose(V*)와 역행렬이 같다.
*Conjugate transpose: 복소수 정사각 행렬의 conjugate의 transpose한 matrix.
- diagonal matrix
- low-rank factorization P, Q
(*자세한 증명은 Appendix C 참고)
Deep S4 Layer
논문의 저자들이 NPLR을 제시한 이유는, HiPPO matrix에 대해서도 S4의 구조가 잘 적용될 수 있도록 하기 위함이다.
즉, general하게 모든 SSM 관점에서 (HiPPO matrix도 포함) diagonalization을 통해서 A를 V ^(-1)AV와 처럼 표현하기 위해 NPLR을 도입했다고 생각해볼 수 있다.


따라서, NPLR을 Lemma 3.1에 대입하게 된다면 SSM은 (A, B, C) ~ (Diagonal - PQ*, B, C)로 재정의 할 수 있다.
즉, S4는 총 5개의 trainable parameters(P, Q, B, C, diagonal)를 훈련하게 된다!
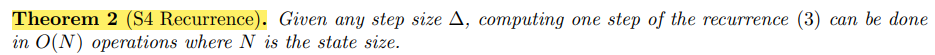

- 시간 복잡도가 획기적으로(?) 줄어드는 것을 확인할 수 있다!
- 특히 S4 Recurrence의 경우 O(N)으로 정의가 된다.
Result
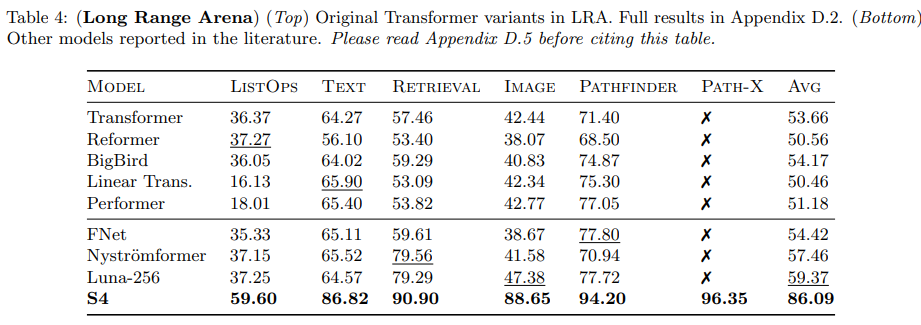
- LRA에서도 좋은 성능을 보이고 있다.
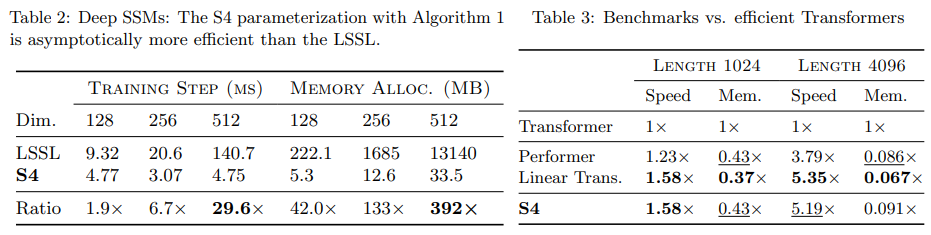
- 기존의 모델과, 이전의 SSM과 비교했을 때, 속도가 많이 향상되었다.
Furthermore
Mamba 논문 리뷰: https://kyujinpy.tistory.com/149
[Mamba 논문 리뷰 4] - Mamba: Linear-Time Sequence Modeling with Selective State Spaces
*Mamba 논문 리뷰 시리즈3 입니다! 궁금하신 점은 댓글로 남겨주세요!시리즈 1: Hippo시리즈 2: LSSL시리즈 3: S4시리즈 4: Mamba시리즈 5: Vision MambaMamba paper: https://arxiv.org/abs/2312.00752 Mamba: Linear-Time Sequence
kyujinpy.tistory.com
*드디어 대망의 하이라이트인 mamba 논문 리뷰를 위해서 가시죠!
- 2024.06.27 Kyujinpy 작성.
*광고 수익은 연말에 기부를 할 생각입니다! 감사합니다.



