*Mamba 논문 리뷰 시리즈4 입니다! 궁금하신 점은 댓글로 남겨주세요!
시리즈 1: Hippo
시리즈 2: LSSL
시리즈 3: S4
시리즈 4: Mamba
시리즈 5: Vision Mamba
Mamba paper: https://arxiv.org/abs/2312.00752
Mamba: Linear-Time Sequence Modeling with Selective State Spaces
Foundation models, now powering most of the exciting applications in deep learning, are almost universally based on the Transformer architecture and its core attention module. Many subquadratic-time architectures such as linear attention, gated convolution
arxiv.org
Mamba github: https://github.com/state-spaces/mamba
GitHub - state-spaces/mamba: Mamba SSM architecture
Mamba SSM architecture. Contribute to state-spaces/mamba development by creating an account on GitHub.
github.com
Contents
- Selective Copying & Induction Heads
- SSM + Selection (S6; Selective SSM)
- Efficient Implementation of Selective SSM
Simple Introduction

Transformer가 모든 분야를 장악한 이후, 아마 대부분 연구자들의 공통된 관심사 중 하나는 'Transformer를 뛰어넘는 혹은 대체 가능한 아키텍쳐가 나올 것인가?'이라고 생각한다.
바로 Mamba가 Transformer를 대체할 혹은 뛰어난 아키텍쳐라고 불리고 있다!
물론, transformer의 여러 단점들이 기술이 발전되고, GPU가 발전됨에 따라 조금씩 줄어들고 있지만,
Mamba는 확실히 매력적이고, 앞으로 계속해서 발전시키고 연구를 이어나가야 할 차세대 아키텍쳐임을 틀림없다!
기존 SSM의 단점들을 어떻게 극복하고, Mamba는 무엇인지 한번 알아봅시다!
Background Knowledge: S4
S4 논문리뷰: https://kyujinpy.tistory.com/148
[Mamba 논문 리뷰 3] - S4: Efficiently Modeling Long Sequences with Structured State Spaces
*Mamba 논문 리뷰 시리즈3 입니다! 궁금하신 점은 댓글로 남겨주세요!시리즈 1: Hippo시리즈 2: LSSL시리즈 3: S4시리즈 4: Mamba시리즈 5: Vision MambaS4 paper: [2111.00396] Efficiently Modeling Long Sequences with Structured
kyujinpy.tistory.com
*이전의 논문리뷰에 이어서 진행됩니다!
*이전의 모델이 가진 장점과, SSM 모델들의 단점들을 어떻게 극복했는지 보면서 글을 이해하시면 더욱 좋을 것 같습니다!
Method
Two Limitations about SSM

일단 기본적으로, State Space Model(SSM)은 시간 불변성(Linear Time Invariance, LTI)을 가지고 있습니다.
즉, 모든 시간 스텝에 대해서, A, B, C와 같은 matrix가 고정되어 있습니다!
따라서, 어떠한 입력이 들어가도 transformer와 다르게 LTI(시간 불변) 특성으로 인해 입력값에 따른 연산이 유동적으로 변화하기 힘듭니다.

Mamba 저자들은 위의 문제를 해결하기 위해 2가지 예시를 가져왔습니다.
1. Selective Copying
2. Induction Heads
이제부터 이 각각이 무엇이 한번 살펴봅시다!
Selective Copying & Induction Heads

Selective Copying은 쉽게 풀었으면 아래와 같이 설명할 수 있습니다.
'여러 input tokens 가운데, 선택적으로 token을 골라서 차례대로 출력하는 것'
이것은 LTI를 가지고 있는 SSM에서는 거의 불가능(?) 합니다. 왜냐하면 SSM을 구성하는 state matrix들은 모든 token에 대해서 동등한 역할을 수행하기 때문에 선택적으로 token을 뽑아서 출력하는 건 어려운 작업이 됩니다.
따라서, Selective Copying을 SSM이 수행할 수 있게 된다면 content-aware reasoning (인식-추론)이 가능하게 됩니다!!
Induction Heads는 이전에 발견되었던 패턴을 추출하여 재현하는 것을 말합니다!
이것 또한, content-aware reasoning의 주요한 기능 중 하나이며, 논문의 저자들은 2가지 문제에 대해서 해결하는 SSM 알고리즘 제안하게 됩니다!
SSM + Selection (S6; Selective SSM)


Mamba 논문의 저자들은, S4+Selection인 S6(Selective SSM) 구조를 제안했습니다. 구조의 차이점은 아래와 같습니다!
1. B, C, Δ의 파라미터 shape 조절.
- D는 input의 dimension; N은 새로운 hidden dimension
- 기존 S4에서는 (D, N)이었다면, S6에서는 (B, L, N)으로 변경
- 각 batch마다 length가 L로 변경됨.
2. Time-invariant에서 time-varying 관점으로 바뀜.
- 기존에는 입력값에 항상 고정된 state matrix A, control matrix B, output matrix C로 연산을 진행했기 때문에 모든 토큰에 동등한 역할 수행 (LTI; 시간 불변성)
- 그러나, 전체적인 상태는 정적인 state matrix A로 구성하고, control matrix B와 output matrix C를 조절함으로써 각 state에 동적인 영향성을 부여할 수 있게 됨.
- 더 나아가서, discretization parameter Δ를 조절하여 각 입력에 따라 서로 다른 step을 주어 적절하게 토큰의 관계를 해석할 수 있도록 함.
What is Discretization


- Discretization에 대한 부분은 시간 step에 따른 중요성을 강조하기 위한 matrix 정도로 생각하시면 편합니다!
- 시간 step을 나눈다는 표현보다는 위의 표현이 직관적으로 이해하시기에 편하실 것 같은데요..!
- 사실 Discretization에 나온 이유는, dynamic linear system에서 continous functions이 아닌 discrete functions을 다루기 위해서 나온 ZOH(zero-order hold) 방법을 SSM에서는 주로 사용합니다.
- 이전의 SSM 연구에서 ZOH를 활용하면, normalization 효과와 resolution에 대한 불변성 효과를 얻을 수 있다고 언급하고 있습니다.
[참고 Reddit 자료]: [D] What on earth is "discretization" step in Mamba? : r/MachineLearning (reddit.com)
Efficient Implementation of Selective SSM
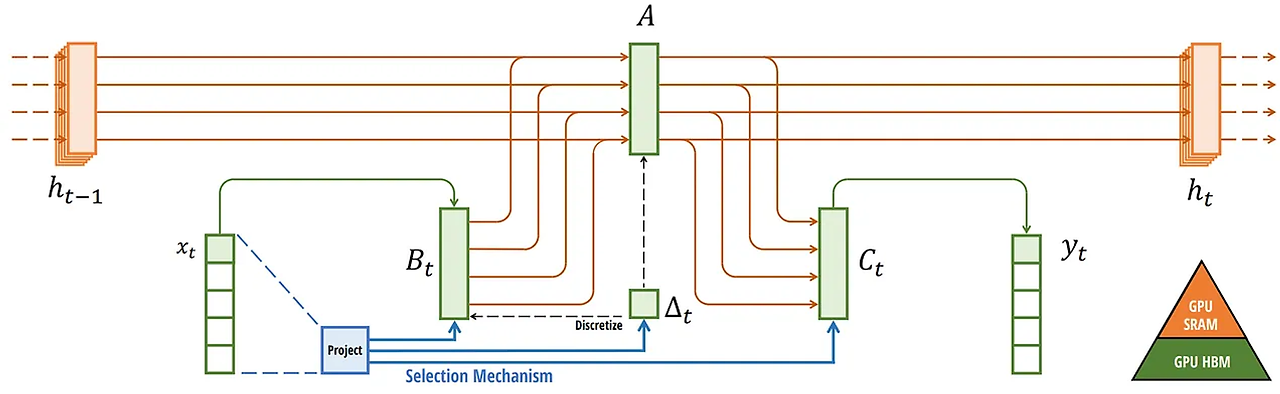
Selective SSM에서는 동적인 커널 B, C를 이용하기 시작했습니다.
따라서 convolution과 같이 고정된 커널을 활용하지 못하게 되었고, 이에 대한 하드웨어 제약도 생기지 시작했습니다.
이러한 현상을 방지하기 위해서, Mamba는 flash-attention과 같이 하드웨어적인 측면에서 matrix를 할당하고 풀면서
메모리 overflow 현상을 해결했습니다!
*(자세한 부분은 논문을 참고해주세요!)
Mamba Architecture

마지막 관문인 mamba block을 살펴보는 과정입니다!
Mamba block은 transformer처럼(?) attention을 정의하고 multi-head attention과 같은 느낌입니다. ㅎㅎ
[Mamba block]
1. Input data가 들어옴
2. Linear projection 적용함.
3. Convolution network 적용
- SiLU (비선형 활성화함수) 적용
4. Selective SSM 적용
5. 마지막으로 linear projection 적용하고, N번 반복!
Mamba Code
# https://github.com/state-spaces/mamba/blob/main/mamba_ssm/modules/mamba_simple.py
class Mamba(nn.Module):
def __init__(
self,
d_model,
d_state=16,
d_conv=4,
expand=2,
dt_rank="auto",
dt_min=0.001,
dt_max=0.1,
dt_init="random",
dt_scale=1.0,
dt_init_floor=1e-4,
conv_bias=True,
bias=False,
use_fast_path=True, # Fused kernel options
layer_idx=None,
device=None,
dtype=None,
):
factory_kwargs = {"device": device, "dtype": dtype}
super().__init__()
self.d_model = d_model
self.d_state = d_state
self.d_conv = d_conv
self.expand = expand
self.d_inner = int(self.expand * self.d_model)
self.dt_rank = math.ceil(self.d_model / 16) if dt_rank == "auto" else dt_rank
self.use_fast_path = use_fast_path
self.layer_idx = layer_idx
# linear projection layer (2개)
self.in_proj = nn.Linear(self.d_model, self.d_inner * 2, bias=bias, **factory_kwargs)
# convolution layer
self.conv1d = nn.Conv1d(
in_channels=self.d_inner,
out_channels=self.d_inner,
bias=conv_bias,
kernel_size=d_conv,
groups=self.d_inner,
padding=d_conv - 1,
**factory_kwargs,
)
# activation function
self.activation = "silu"
self.act = nn.SiLU()
## B, C, ∆를 생성하기 위한 부분 (Selective SSM 알고리즘 참고)
self.x_proj = nn.Linear(
self.d_inner, self.dt_rank + self.d_state * 2, bias=False, **factory_kwargs
)
self.dt_proj = nn.Linear(self.dt_rank, self.d_inner, bias=True, **factory_kwargs)
## Discretization 초깃값
# Initialize special dt projection to preserve variance at initialization
dt_init_std = self.dt_rank**-0.5 * dt_scale
if dt_init == "constant":
nn.init.constant_(self.dt_proj.weight, dt_init_std)
elif dt_init == "random":
nn.init.uniform_(self.dt_proj.weight, -dt_init_std, dt_init_std)
else:
raise NotImplementedError
## A와 delta(dt)의 정의에 대한 궁금증
# 참고: https://github.com/state-spaces/mamba/issues/326
#### 무시해도 되는 부분 ####
# Initialize dt bias so that F.softplus(dt_bias) is between dt_min and dt_max
dt = torch.exp(
torch.rand(self.d_inner, **factory_kwargs) * (math.log(dt_max) - math.log(dt_min))
+ math.log(dt_min)
).clamp(min=dt_init_floor)
# Inverse of softplus: https://github.com/pytorch/pytorch/issues/72759
inv_dt = dt + torch.log(-torch.expm1(-dt))
with torch.no_grad():
self.dt_proj.bias.copy_(inv_dt)
# Our initialization would set all Linear.bias to zero, need to mark this one as _no_reinit
self.dt_proj.bias._no_reinit = True
##############################
## SSM 정의 (A만)
# S4D real initialization
A = repeat(
torch.arange(1, self.d_state + 1, dtype=torch.float32, device=device),
"n -> d n",
d=self.d_inner,
).contiguous()
A_log = torch.log(A) # Keep A_log in fp32
self.A_log = nn.Parameter(A_log)
self.A_log._no_weight_decay = True
## D "skip" parameter (no using)
self.D = nn.Parameter(torch.ones(self.d_inner, device=device)) # Keep in fp32
self.D._no_weight_decay = True
# Output projection
self.out_proj = nn.Linear(self.d_inner, self.d_model, bias=bias, **factory_kwargs)- 위에는 모델의 변수 정의 부분 입니다! 중요한 부분은 아래와 같습니다.
1. self.in_proj: linear projection. (여기서 2개로 쪼개짐.)
2. self.conv1d: convolution network
3. self.x_proj: Selective SSM에 input으로 들어올 x를 기준으로 linear layer를 통과시켜서 B, C, Δ matrix 생성.
4. self.dt_proj: Δ matrix를 한번 더 linear layer에 통과시킴.
# https://github.com/state-spaces/mamba/blob/main/mamba_ssm/modules/mamba_simple.py
def forward(self, hidden_states, inference_params=None):
"""
hidden_states: (B, L, D)
Returns: same shape as hidden_states
"""
batch, seqlen, dim = hidden_states.shape
conv_state, ssm_state = None, None
if inference_params is not None:
conv_state, ssm_state = self._get_states_from_cache(inference_params, batch)
if inference_params.seqlen_offset > 0:
# The states are updated inplace
out, _, _ = self.step(hidden_states, conv_state, ssm_state)
return out
# We do matmul and transpose BLH -> HBL at the same time
### Linear projection 적용해서,
### x와 z 2개 projection vectors 생성
xz = rearrange(
self.in_proj.weight @ rearrange(hidden_states, "b l d -> d (b l)"),
"d (b l) -> b d l",
l=seqlen,
)
if self.in_proj.bias is not None:
xz = xz + rearrange(self.in_proj.bias.to(dtype=xz.dtype), "d -> d 1")
### SSM의 핵섬!
### State matrix A 정의. (논문 수식)
A = -torch.exp(self.A_log.float()) # (d_inner, d_state)
(..중략..)
### chunk를 통해 분리
x, z = xz.chunk(2, dim=1)
### Compute short convolution
if conv_state is not None:
# If we just take x[:, :, -self.d_conv :], it will error if seqlen < self.d_conv
# Instead F.pad will pad with zeros if seqlen < self.d_conv, and truncate otherwise.
conv_state.copy_(F.pad(x, (self.d_conv - x.shape[-1], 0))) # Update state (B D W)
if causal_conv1d_fn is None:
x = self.act(self.conv1d(x)[..., :seqlen])
else:
assert self.activation in ["silu", "swish"]
x = causal_conv1d_fn(
x=x,
weight=rearrange(self.conv1d.weight, "d 1 w -> d w"),
bias=self.conv1d.bias,
activation=self.activation,
)
# We're careful here about the layout, to avoid extra transposes.
# We want dt to have d as the slowest moving dimension
# and L as the fastest moving dimension, since those are what the ssm_scan kernel expects.
### projection layer를 통해서 B, C, dt 정의
x_dbl = self.x_proj(rearrange(x, "b d l -> (b l) d")) # (bl d)
dt, B, C = torch.split(x_dbl, [self.dt_rank, self.d_state, self.d_state], dim=-1)
### dt는 linear layer 한번 더 통과
dt = self.dt_proj.weight @ dt.t()
dt = rearrange(dt, "d (b l) -> b d l", l=seqlen)
B = rearrange(B, "(b l) dstate -> b dstate l", l=seqlen).contiguous()
C = rearrange(C, "(b l) dstate -> b dstate l", l=seqlen).contiguous()
assert self.activation in ["silu", "swish"]
### Selective SSM 적용
y = selective_scan_fn(
x,
dt,
A,
B,
C,
self.D.float(),
z=z,
delta_bias=self.dt_proj.bias.float(),
delta_softplus=True,
return_last_state=ssm_state is not None,
)
if ssm_state is not None:
y, last_state = y
ssm_state.copy_(last_state)
y = rearrange(y, "b d l -> b l d")
### Output projection
out = self.out_proj(y)
return out- 윗부분은 모델의 forward 입니다!
1. Linear projection을 통해서 xz 생성. (x vector, z vector로 이름 붙임)
2. chunk()함수를 통해서 x와 z를 분리. (코드 참고)
3. x를 convolution layer 통과
4. self.x_proj(x): B, C, dt 변수 생성.
5. dt = self.dt_proj.weight @ dt.t() 적용
6. Selective SSM
7. Output projection을 통해서 모델 결과 나옴,
Result

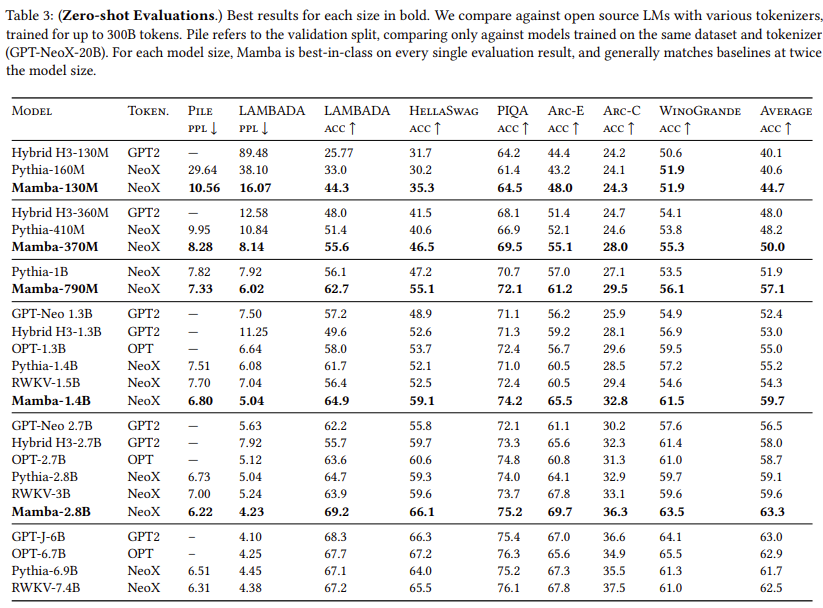
- 2024.07.01 Kyujinpy 작성.
*광고 수익은 연말에 기부를 할 생각입니다! 감사합니다 ㅎㅎ



