*DDIM를 위한 논문 리뷰 글입니다! 궁금하신 점은 댓글로 남겨주세요!
DDIM paper: [2010.02502] Denoising Diffusion Implicit Models (arxiv.org)
Denoising Diffusion Implicit Models
Denoising diffusion probabilistic models (DDPMs) have achieved high quality image generation without adversarial training, yet they require simulating a Markov chain for many steps to produce a sample. To accelerate sampling, we present denoising diffusion
arxiv.org
DDIM github: ermongroup/ddim: Denoising Diffusion Implicit Models (github.com)
GitHub - ermongroup/ddim: Denoising Diffusion Implicit Models
Denoising Diffusion Implicit Models. Contribute to ermongroup/ddim development by creating an account on GitHub.
github.com
Contents
- Non-Markovian Forward process
- Generative Process and Unified Variational Inference Objective
- Sampling From Generalized Generative Processes
Simple Introduction

DDPM이 나온 이후, DDPM보다 더 효율적이고 더 빠르게 작동되는 DDIM이 나타났다.
기존의 Diffusion-Denoising process는 markovian을 기반으로 작동되는 메커니즘이었지만, DDIM은 non-markovian으로 움직인다.
어떻게 작동되는지 수식으로 알아보고, DDIM을 이해해보자!
Background Knowledge: DDPM
DDPM 논문 리뷰: https://kyujinpy.tistory.com/95
[DDPM 논문 리뷰] - Denoising Diffusion Probabilistic Models
*DDPM를 위한 논문 리뷰 글입니다! 궁금하신 점은 댓글로 남겨주세요! DDPM paper: https://arxiv.org/abs/2006.11239 Denoising Diffusion Probabilistic Models We present high quality image synthesis results using diffusion probabilistic m
kyujinpy.tistory.com
- Diffusion 및 DDPM에 대해서 먼저 이해하고 오셔야 이해하실 수 있습니다!
Method
Non-Markovian Forward process

DDIM과 DDPM을 간단히 비교하면 위와 같이 표현할 수 있따.
Marginal distribution은 같지만, inference distribution에서 DDPM은 markovian인 반면에, DDIM은 non-markovian으로 표현되고 있다
즉 DDPM에서는 markovian으로 인해 xt는 xt-1로 부터 결정되었다면, DDIM에서는 xt와 x0를 같이 이용해서 xt-1을 결정하게 된다.

Forward process는 베이지안에 따라서 위와 같이 표현될 수 있다.
여기서 sigma는 모델의 stochastic 정도를 결정하는데 0에 가까워질 수록 determinstic해진다! (확실하게 알 수 있다!)
그리고 눈치 채신 분도 있겠지만, q분포의 xt가 xt-1와 x0를 의존하기 때문에 더이상 markovian이 아니다!
Generative Process and Unified Variational Inference Objective

Generative process의 초반 설명이다!
이제 p분포를 학습하고자 하는데, 여기서는 q분포의 값을 토대로 학습을 진행한다.
즉, xt-1은 noise한 xt가 있을 때 x0를 이용해서 xt-1을 sampling하는 방식으로 진행된다!

그러기 위해서는 일련의 과정을 통해서 수식을 전개해야 한다.
1. Equation (4)를 이용해서 x0로 부터 바로 xt를 만들어준다. (Diffusion에서 많이 보던 수식 ^^)
2. Ⲉ()은 xt로 부터 noise 값인 Ⲉt를 예측하는 것이다. (DDPM에서 사용했던 reparameterization 방법과 유사한 듯)
3. Equation (4)로 부터 Equation (9)를 전개할 수 있다. (좌변이 x0가 아닌 이유는?!)

위의 3번에 대한 질문에 대한 답변은 x0를 prediction하는 것이 목적이기 때문에 eplison값을 함수로 정의해서 x0를 예측하겠다는 의미로 받아들일 수 있다.
즉, f(xt)는 어떠한 xt에 대해서 x0를 예측하는 함수인 것이다.
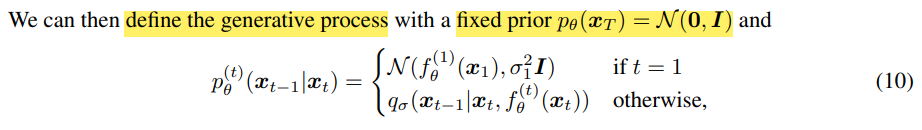
위의 수식을 바탕으로 정의된 generative process이다.
t=1일 때는 gaussian noise를 더해주는 형태로 표현이 되는데, 이는 논문에서 generative process가 어디에서나 잘 supproted할 수 있도록 ensure해준다고 말해주고 있다.
Otherwise의 경우에는 f(xt)와 xt값을 이용해서 xt-1을 sampling하는 것으로 생각하면 된다.

Generative process를 최적화 시키기 위해 이용되는 variational lower bound의 형태이다.
해당 논문에서는 sigma를 어떻게 선택하느냐에 따라서 differenct variational objective가 되는데,
만약, sigma가 0보다 크다면 DDPM의 ELBO와 같은 형태가 되고, 0이면 DDIM의 objective이다.
-> 즉 DDIM에서는 non-markovian을 위해서 sigma를 0으로 설정한다!!!
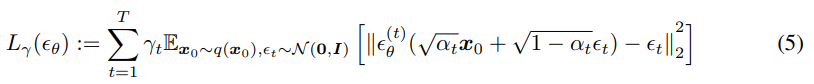

+) 위의 generative process의 variational lower bound에 대한 이론적 설명이다.
(-> 해당 부분은 잘 이해가 안된다..ㅎㅎ)
Sampling From Generalized Generative Processes
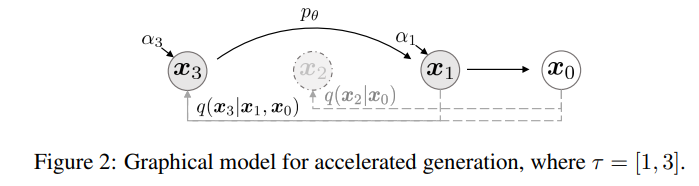
DDIM의 sampling 방법을 나타낸 그림이다!
어떻게 DDPM보다 빠르게 sampling이 가능한지 한번 살펴보자.
Denoising Diffusion Implicit Models
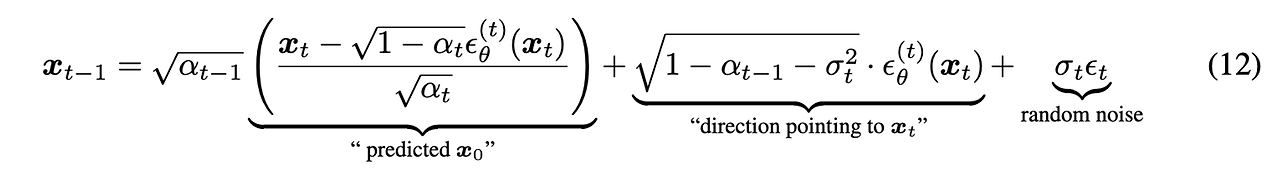

DDIM의 설명은 다음과 같다. (Equation 12)
1. 일단 위에서 정의된 generative process와 기존에 정의되어 있던 forward process의 수식을 바탕으로 Xt-1이 sampling되는 과정을 적을 수 있다.
2. 여기서 만약 sigma가 0이 아니라면, markovian에 따라서 DDPM이 된다.
3. 그러나 sigma가 0이라면, random noise가 0이 되기 때문에 XT에서 X0로 sampling되는 과정이 고정된다!!
여기서 한가지 짚고 넘어갈 중요한 포인트가 있다.
1. DDIM은 새로운 훈련 방법보다는 DDPM에서 만들어진 objective를 non-markovian chain으로 generalize하게 만들어서 sampling하는 방법을 제시했다는 것이다.
2. Sigma의 값이 사실 DDIM의 핵심이라고 느껴지지만 이것은 어디까지나 generation에 포커스가 있고, DDPM과 DDIM 모두 Ⲉtθ에서 parameter인 θ를 예측하는 것이 학습의 목적이다.
3. 따라서 DDPM으로 훈련하고, DDIM으로 generation하는 것이 요즘 트렌드이다.
Accelerated Generation Processes

따라서, Forward process가 T steps를 가지고 있다해도, L1까지 가는 sampling 과정에서 더이상 특정한 forward 과정이 고려되지 않기 때문에, 더 적은 steps으로 충분히 generation할 수 있다는 점이 포인트이다!!
(왜냐하면 q_sigma(xt|x0)가 고정되어 있기 때문이다.)
Result


- 2023.08.15 Kyujinpy 작성.
+) 다음에는 코드 리뷰로 돌아오겠습니다!



