*DDPM를 위한 논문 리뷰 글입니다! 궁금하신 점은 댓글로 남겨주세요!
DDPM paper: https://arxiv.org/abs/2006.11239
Denoising Diffusion Probabilistic Models
We present high quality image synthesis results using diffusion probabilistic models, a class of latent variable models inspired by considerations from nonequilibrium thermodynamics. Our best results are obtained by training on a weighted variational bound
arxiv.org
DDPM github: https://github.com/lucidrains/denoising-diffusion-pytorch
GitHub - lucidrains/denoising-diffusion-pytorch: Implementation of Denoising Diffusion Probabilistic Model in Pytorch
Implementation of Denoising Diffusion Probabilistic Model in Pytorch - GitHub - lucidrains/denoising-diffusion-pytorch: Implementation of Denoising Diffusion Probabilistic Model in Pytorch
github.com
Contents
Simple Introduction
드디어 미루고 미루던, 컴퓨터 비전의 혁명(?) Diffusion을 논문리뷰를 한다.
Diffusion model이 나올 때부터 굉장히 관심이 많았고, diffusion을 활용하여 나만의 generative AI를 만들고 싶은 생각도 있는데..(향후 계획으로 ㅎㅎ)
Diffusion이 무엇인지 한번 파고 들어가보자!
Background Knowledge: VAE
VAE 논문리뷰: https://kyujinpy.tistory.com/88
[VAE 논문 리뷰] - Auto-Encoding Variational Bayes
*VAE 수학적 지식을 리뷰하기 글입니다! 궁금하신 점은 댓글로 남겨주세요! *(통계학, 확률론 지식이 있다고 가정합니다.) VAE paper: https://arxiv.org/pdf/1312.6114.pdf Contents 1. Simple Introduction 2. Mathematical M
kyujinpy.tistory.com
- VAE와 score-based generative model의 관점이 둘다 있지만, VAE에 대한 명확한 이해가 있어야 수식을 유도하는데 도움이 됩니다!
Method
Diffusion

Diffusion에서 중요한 개념은 바로 'Stochastic Process' 이다.
이것은 time-dependent variables을 통해서 이루어진다는 것이다.
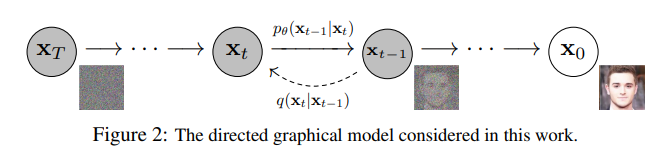
Diffusion을 간략하게 살펴보면, Backward, Forward process가 있다.
Backward process는 noise에서 이미지로 가는 것이고,
Forward process는 이미지에서 noise로 가도록 하는 것 이다.
여기서 Backward process를 training하는 것이 바로 Diffusion model인 것이다!
Forward process
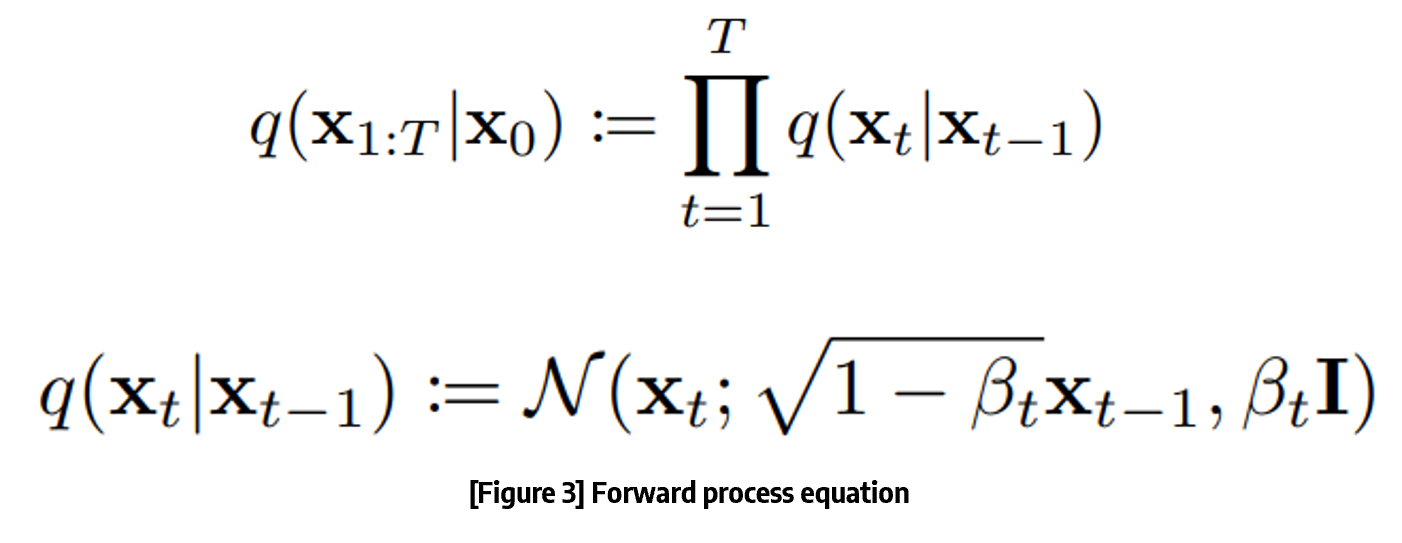
Forward process는 위의 수식으로 표현이 가능합니다!
일단 Forward process는 Diffusion process라고도 불립니다.
그 이유는, gaussian distribution에서 나온 noise를 더해주는 과정이기 때문입니다.
일단 q(x1:T|x0) 수식을 보면 '우도(likelihood)'의 형태를 보이고 있다는 것을 알 수 있다.
또한 밑에 조건부 확률의 수식을 보면, gaussian distribution에서 값을 추출한다는 것을 알 수 있다.
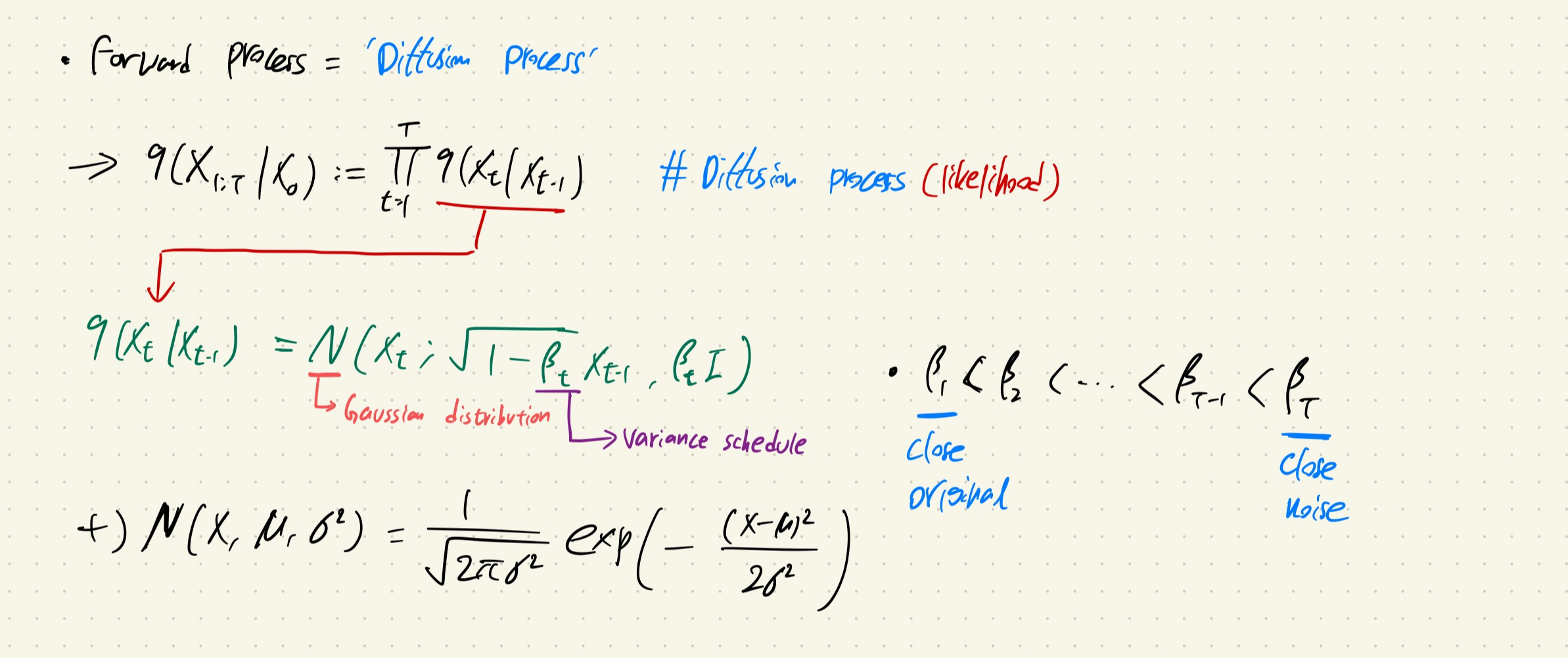
위의 수식에서 β는 diffusion rate(variance schedule)로 분산이 divergence하는 것을 방지해줍니다. Scaling의 역할입니다.
또한 β1 < ... < βT의 조건을 만족해야하는데, β1은 original image에 가까운 수준이고, βT는 nosiy image에 가까워야 하기 때문입니다. (Gaussian distribution의 noise를 더해가면서 original image와 거리가 멀어져야하기 때문이다.)
다만 위의 β를 이용해서 수식을 전개할 때 단점이 있습니다.
X0(original image)에서 XT(noisy image)로 전개할 때, 0~T의 모든 수식을 step by step으로 전개해야되기 때문입니다.
이는 memory를 많이 소모하게 되고, 시간도 오래걸리는 단점이 있습니다.
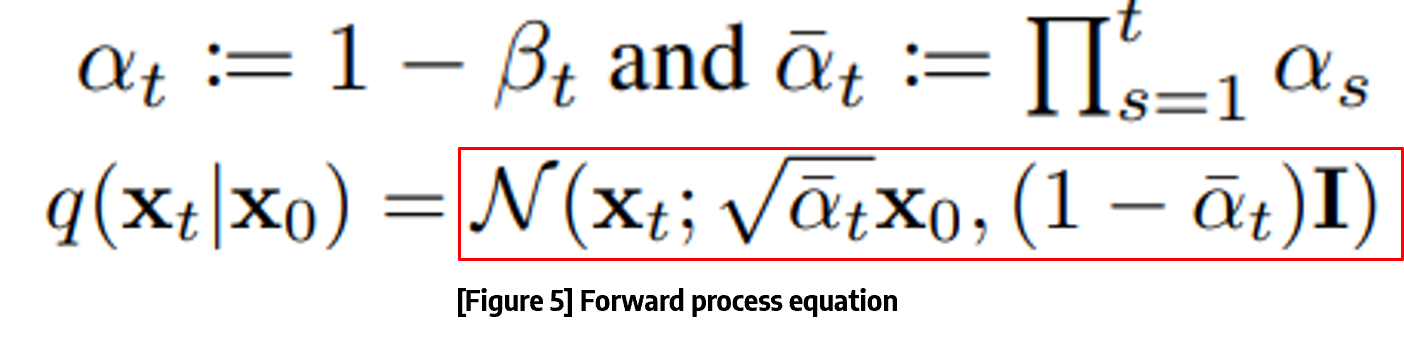
위의 문제점을 해결하기 위해서는 α를 이용하면 됩니다!
좀더 자세히 살펴봅시다.

Xt는 gaussian distribution에서 나오는 값이기 때문에 평균을 기준으로 어느정도 분산으로 치우친 값을 가질 것입니다.
따라서 Xt = √(1-βt)xt-1 + √(βt)로 표현이 가능합니다.
여기서 αt=(1-βt)로 표현을 하게 된다면, 위의 수식에서 보는 것과 같이 X0에서 Xt로 한번에 전개가 가능합니다!
+) 추가적으로 Z는 N(0,1)을 따르는 값인데, 이는 기존 equation의 I와 다를 것이 없습니다.

+) 위의 Forward process를 정리하면, 위의 사진처럼 표현이 가능합니다!
+) 한번 되새기면서 생각해보세요!!
+) 중요한 point는 Gaussian distribution을 활용해서 noise를 더해간다는 점과, α를 이용하여 X0에서 XT를 만드는 과정(Forward process의 전개 과정)을 한번에 sampling할 수 있다는 점입니다!

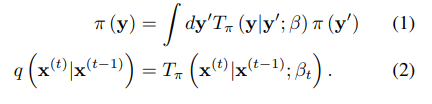

+) Diffusion 논문에서 소개하는 식
+) 여기서는 Gaussian distribution으로 noise를 더하는 걸, Markov diffusion kernel로 표현했다.
+) Eqaution 3이 T steps of diffusion을 표현한 것이다.

Backward process

Diffusion의 꽃인 Backward process(Reverse process)입니다!
Backward process의 경우 VAE와 동일하게 model의 log likelihood를 maximizing하는 것에 초점을 둡니다.

일단 VAE와 동일하게 ELBO를 찾고 이를 최대화 하는 방향으로 훈련을 진행합니다.
Diffusion에서는 equation (3)을 loss function으로 활용하여 훈련을 진행하는데, 이를 효율적으로 바꾸기 위해서 Equation (5)처럼 표현합니다.



Equation (3)에서 Equation (5)의 전개 과정은 위의 식과 같습니다!
1. Backward process의 정의에 의해서 수식1로 분해가 가능합니다.
2. t=0일 때의 negative log likelihood를 따로 분리합니다.
3. Markov chain의 특징과 bayes rule을 활용하여 적절한 항을 만듭니다.
4. KL-divergence 정의를 이용하여 최종적인 수식을 만듭니다.

+) 마지막 항은 Loss funciton으로 3가지 의미를 담고 있다.
+) First loss term(LT): KL-divergence를 통해서 X0로 XT를 생성하는 q분포와 p(XT)의 분포가 유사해지도록 합니다.
+) Second loss term(L1:T-1): reverse process와 diffusion process 간의 분포가 유사해지도록 합니다.
+) Third loss term(L0): reconstruction loss로 x1에서 x0(original image)가 나올 우도를 최대화합니다.
DDPM(Diffusion Denoising Probability Model)

마지막 목표인 DDPM까지 왔다!
사실 요즘에는 DDPM보다 DDIM을 더 자주 사용하는데, 추후 논문리뷰로 남겨놓겠다.
DDPM은 기존의 diffusion 방식을 보다 빠르고 적은 cost로 training시킬 수 있는 trick?을 소개한다.
Forward Process

기존의 DIffusion model을 다시 생각해보자.
Forward process와 backward process가 있었다.
여기서 backward process는 당연히 trainable하다. 또한 Forward process도 trainable 하다.
Forward process에서 중요한 parameter인 β는 trainable하게 훈련되었다.
그러나 DDPM에서는 β를 constant하게 유지하여서 Forward process를 훈련할 필요가 없게 만들었고, 이 결과 위에서 마지막으로 봤던 First loss term(LT)를 무시할 수 있게 되었다.

Reverse Process


Reverse process (1<t<T)인 구간에서 DDPM은 2가지 방법을 제시한다.
첫번째는 분산과 관련된 조건이다.
Reverse process에서 sampling을 할 때, gaussian distribution의 분산을 위의 2가지 방식으로 설정하는 것이다.
첫번째 경우에는 x0가 N(0,I)로 최적화되고, 두번째 경우에는 one point로 최적화된다고 언급하고 있다.
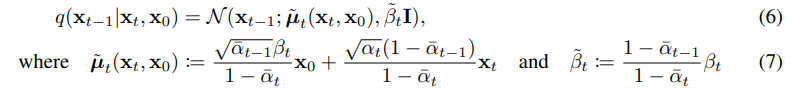

두번째는 평균과 reparameterizing을 이용하여 loss function을 design하는 것이다.
Equation (4)에서 소개되었던(위에서도 언급함) αt=(1-βt)를 이용하여서 reparameterizing을 하는 것이다.
Equation (10)의 경우 Equation (7)에 근거하여서 변환할 수 있다.
여기까지 보면 아직 무슨 얘기를 하는지 잘 모를 수도 있다, 밑에 사진을 한번 보자.


Equation 10을 보면 해당 식은 p 분포의 평균이 q분포의 평균을 예측하는 것으로 생각할 수 있다.
즉, 다르게 생각하면, p분포를 q분포를 기반으로 parameterization해서 얻을 수 있다면 더욱 간단할 것이다!
여기서 Xt는 Forward process에서 얻을 수 있고, 우리가 알고자 하는 것은 eplision Ⲉ ~ N(0,1)이다.
즉, re-parameterization을 이용해서 Ⲉθ(xt, t)라는 함수로 xt가 주어졌을 때 xt-1을 만들기 위해서 필요한 eplision 값을 예측하는 방향으로 design하면 된다!!

+) 위에서 언급했던 α를 이용한 xt표현 방법 리마인드

+) 임의의 noise eplison을 학습하는 방향으로 Diffusion을 수정함으로써 기존보다 훨씬 빠르게 좋은 퀄리티를 만들어낼 수 있다.
Loss function

기존의 Diffusion보다 loss function이 매우 간결해졌다.
기존의 Diffusion은 L0, L1:T-1, LT으로 구분되었다면, DDPM에서는 하나의 simple한 수식으로 표현된다.
그 이유는 위에서 다 언급했지만 가장 큰 이유는 βt가 고정되어 있기 때문이다.

+) 위에서 언급된 equation 13은 t=1일 때, reverse process의 모습을 보여주고 있다.

+) 논문에서 활용한 beta 값과 T값, 그리고 image scaling 값이다.
Result


- 2023.08.04 Kyujinpy 작성.
*질문이나 오타 등등은 댓글로 남겨주세요 ㅎㅎ



