Complex eigenvalues - conjugation, linear transformation

Conjugation

Complex eigenvalues에는 매우 특이한 성질이 있다.

1. Eigenvalues간의 conjugation이 있다.

2. Eigenvectors간의 conjugation이 있다.

 

따라서 하나의 eigenvalues, eigenvectors를 구한다면, 다른 eigenvalue, eigenvector를 구할 수 있다.

 

Linear transformation

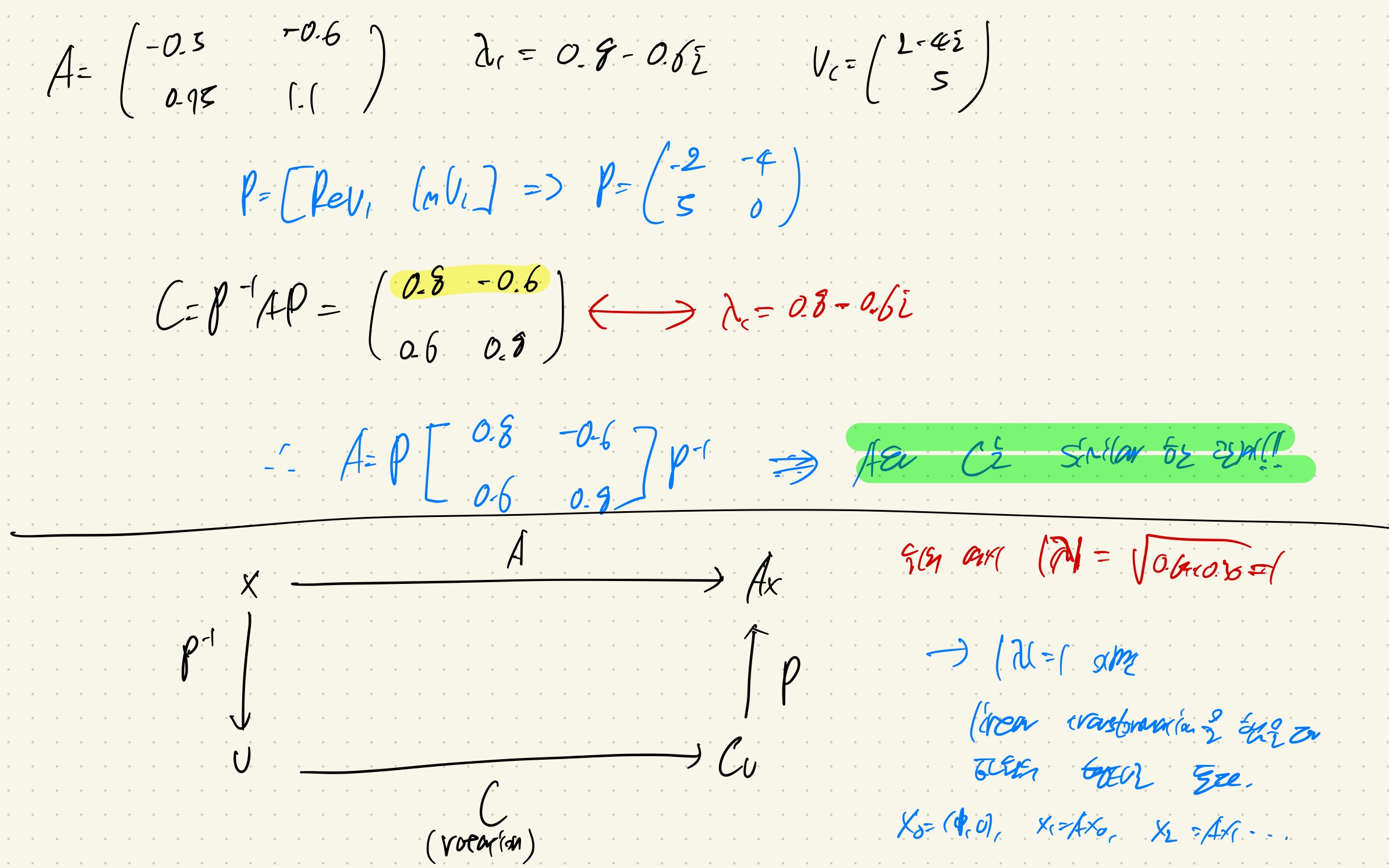
C라는 matrix가 linear transformation 중 rotation을 하는 역할이라고 생각해보자.

이때 C=P^-1AP라고 할 때, C는 eigenvalues  = a - bi의 형태에서 a와 b로 이루어진 matrix 형태가 된다.

 

그리고 A와 C는 similar한 matrix이다.

 

C의 모습과 eigenvalue의 크기에 따라서 Ax의 형태를 무한히 linear transformation할 때 모습이 달라진다.

x0 = (1,0)

x1 = Ax0

x2 = Ax1

...

이런식으로 linear transformattion이 진행된다 했을 때,

https://raw.githubusercontent.com/NeuromatchAcademy/precourse/main/tutorials/W0D3_LinearAlgebra/static/complex_eigenvalues.gif

|λ| = 1 이면, 타원형의 형태로 무한히 반복된다는 것을 알 수 있고,

|λ| < 1 이면, 안으로 들어가는 형태,

|λ| > 1 이면, 밖으로 뻗어나가는 형태로 된다는 것을 알 수 있다.

 

(예시의 gif는 이산적인 값에 대해서 그린 것이라서 각이 보이지만, 실제로는 타원형처럼 곡선의 형태로 그려진다.)