* 이 글은 NeRF에 대한 논문 리뷰이고, 핵심만 담아서 나중에 NeRF Code를 이해할 때 쉽게 접근할 수 있도록 정리한 글입니다.
* 코드와 함께 보시면 매우 매우 도움이 될 것이라고 생각이 들고, 코드 없이 읽으셔도 NeRF를 정복하실 수 있을 것입니다.
NeRF논문 원본: https://arxiv.org/abs/2003.08934v2
NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis
We present a method that achieves state-of-the-art results for synthesizing novel views of complex scenes by optimizing an underlying continuous volumetric scene function using a sparse set of input views. Our algorithm represents a scene using a fully-con
arxiv.org
(D-)NeRF kyujinpy: https://github.com/KyujinHan/NeRF_details_code_analysis
GitHub - KyujinHan/NeRF_details_code_analysis: NeRF code analysis
NeRF code analysis. Contribute to KyujinHan/NeRF_details_code_analysis development by creating an account on GitHub.
github.com
NeRF github: https://github.com/yenchenlin/nerf-pytorch
GitHub - yenchenlin/nerf-pytorch: A PyTorch implementation of NeRF (Neural Radiance Fields) that reproduces the results.
A PyTorch implementation of NeRF (Neural Radiance Fields) that reproduces the results. - GitHub - yenchenlin/nerf-pytorch: A PyTorch implementation of NeRF (Neural Radiance Fields) that reproduces ...
github.com
Contents
1. Simple Introduction
2. Background Knowledge: Camera Parameters
3. Background Knowledge: Ray (directions)
5. Normalized Device Coordinate
Simple Introduction

기존의 논문들은 2D view를 통해서 3D rendering view를 생성을 하기 위해서 여러 노력과 방법을 적용했다.
기존의 방법들은, 성능이 안 좋거나, 너무나 많은 메모리를 요구한다는 단점으로 인해서 실생활에 적용시키기 어려웠다.
NeRF는 이러한 문제점들을 해결하여, 적은 메모리로도 높은 성능의 3D rendering을 할 수 있는 방법을 소개하고 있다.
MLP network와 Camera parameters(theta, phi, angle,...)를 이용하여 학습되지 않은 view에서도 3D rendering을 할 수 있도록 한다.
Background Knowledge: Camera Parameters
1. Pinhole camera

Pinhole camera를 통해서 상이 맺히는 모습이다.
렌즈처럼 큰 원형 렌즈를 하나의 점으로 생각한 카메라 모형이 바로 Pinhole camera이다.
Intrinsic parameters와 Extrinsic parameters를 이용해서 transformation matrix를 만든 후, Image plane에 맺힌 상을 Real world의 좌표로 변환시켜서 표현하는 것이 NeRF의 목적이라고 말할 수 있다. (밑에서 더 자세히 언급)
2. Camera Intrinsic parameters (matrix)

Pinhole camera가 Real wolrd에 있는 물체가 어떻게 카메라의 Image plane에 맺히는지 알려주는 과정이다.
이 과정을 보는 이유는, NeRF는 Image plane에서 Real world로 만들어주는 모델이기 때문에, Intrinsic parameter를 이용한 matrix를 역순으로(역행렬) 계산만 해주면 된다.
위의 사진에서 (X, Y, Z)는 Real world의 좌표, 그리고 중간에 있는 (u, v, 1)은 Normalized plane, 그리고 (x, y, 1)은 Image plane이다.
그렇다면 Intrinsic parameter는 무엇일까?
쉽게 말하면, 카메라 내부 파라미터라고 할 수 있다.
위의 사진을 보면 K가 Intrinsic parameter이다.
K는 Normalized plane에 위치한 상을 Image plane으로 매핑시킬 때 dot product를 진행하는 matrix이다.
(위의 사진에서는 역행렬로 곱하여서, Image plane에서 Normal plane을 만들어 주고 있는데, 아래의 사진을 보면서 자세히 이해해 보자)

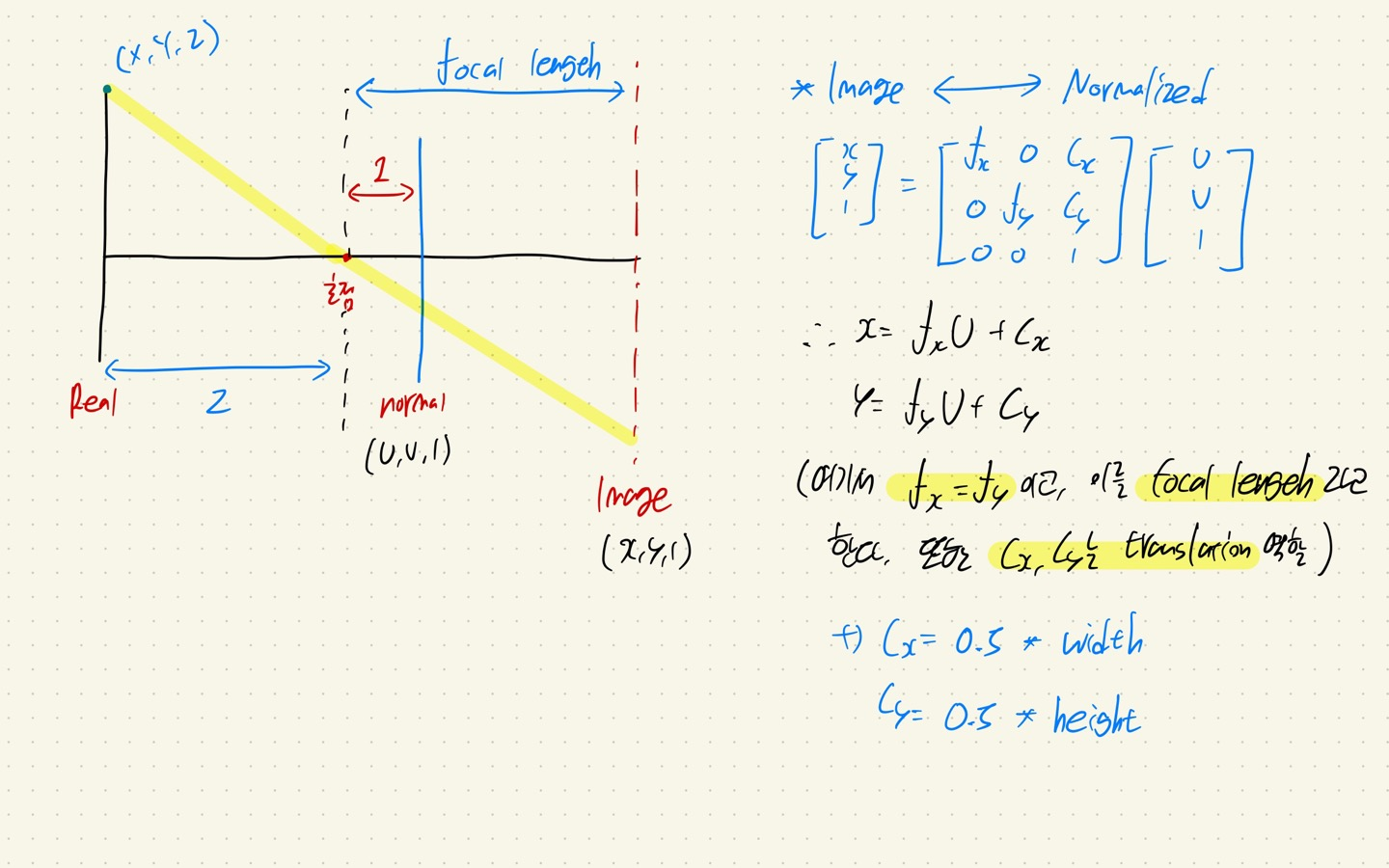
Intrinsic parameters matrix인 K를 자세히 살펴보면 위와 같은 형태로 구성이 된다.
K는 f(focal length)와 C로 구성이 된다.
Focal length는 초점과 Image plane 사이의 거리를 의미한다.
또한 C는 translation에 대한 정보이다.
왜 이것들이 사용되는지 차근차근 정리를 하면서 가보겠다.
2-1. C의 역할
Real world와 Image plane 좌표계에서 이미지의 왼쪽 상단의 좌표가 (0,0)이다.
그러나 Normal plane에서는 이미지의 중앙의 좌표가 (0,0)이다.
즉 Normalized plane -> Image plane으로 오는 과정에서, translation이 일어나게 된 것이다.
따라서, (x, y) 좌표를 0.5*width, 0.5*height 만큼 translation 해주는 상수항이 필요하게 된다.
이 역할을 Cx, Cy가 하는 것이다. 그래서 코드에서 각각 Cx = 0.5*width, Cy = 0.5*height가 된다.
* Camera 좌표계에서는, 위의 사진처럼 사물을 관통하는 직선이 Z 축이다.
* Normalized plane은 Real world와 삼각형 닮음비를 이용하여 계산할 수 있고, Normalized plane을 만들어서 사물이 Z=1인 지점에 위치해 있다고 설정하여 쉽게 transformation이 되도록 해준다. (초점 기준에서는 z = -1)
2-2. Focal length의 역할
Normalized plane과 Image plane의 상의 크기를 보면 삼각형의 닮은 비를 이용해서 풀 수 있다는 것을 알 수 있을 것이다.
그래서 Focal length를 각각 U, V에 곱해주는 것이다.
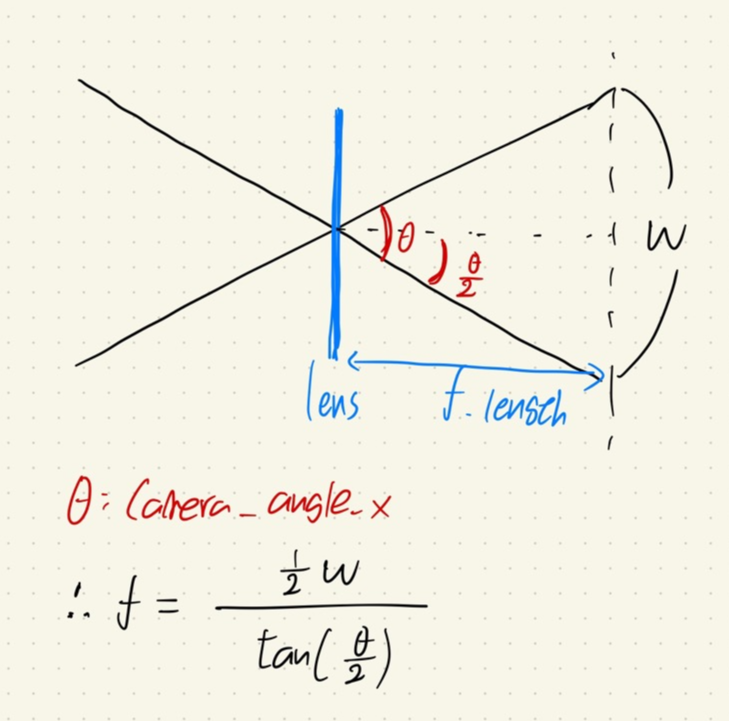
Focal length는 Camera_angle_x와 width를 이용해서 구할 수 있다. (위의 수식을 코드에서도 이용)
*요즘 카메라들은 fx와 fy의 값이 거의 동일하기 때문에 같은 값으로 취급한다.
2-3. Image plane to Normalized plane
Camera의 목적이 Real world -> Normalized plane -> Image plane이라면, NeRF의 목적은 Image plane -> Real world이다.
이때 Image plane에서 Normalized plane으로 가기 위해서, K의 역행렬을 구해도 되지만, x = fx * U + Cx라는 식에서 우리는 U = (x - Cx) / fx를 유도할 수 있다.
그래서 실제 코드에서도, 역행렬을 이용하는 방법보다, 간단한 equation을 푸는 정도로 Normalized plane을 계산한다.
3. Camera Extrinsic parameters (matrix)
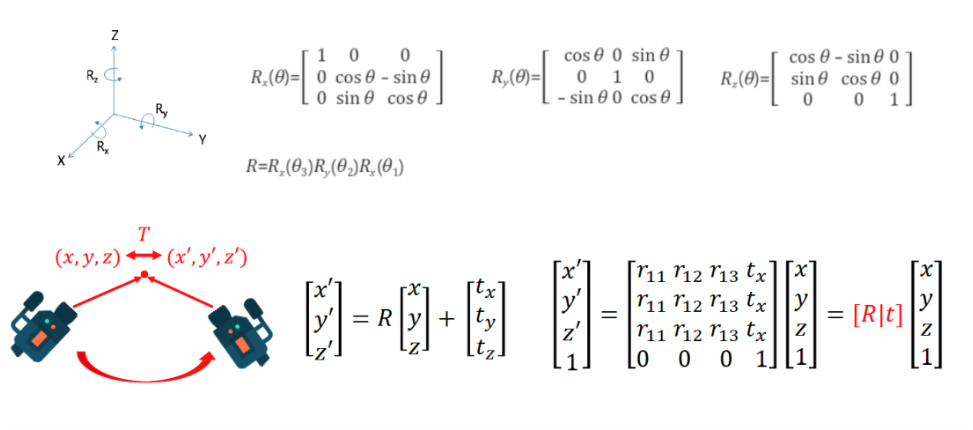
Camera Extrinsic parameters는 쉽게 얘기하면, 카메라 외부 파라미터이다.
즉, Real world에서 찍은 카메라의 theta(방위각), phi(고도각)을 가진다. (theta는 좌우 각도, phi는 위아래 각도라고 생각하면 이해가 편하다..!)
Camera Extrinsic parameters는 Camera coordinates(좌표계)에서 Real World to Camera(W2C)인 파라미터이다.
즉 Real world를 Image Plane으로 만들어줄 때 이용하게 된다.
그런데, NeRF는 Camera to Real World(C2W)인 파라미터를 통해서, Camera coordinates를 Real coordinates로 변경해줘야 하는데 어떻게 진행될까?
일단 똑같이 theta(방위각)과 phi(고도각) 정보는 있어야 한다.
그리고 theta와 phi 정보를 이용해서 3D transformation에서 각 축을 이동할 때 이용하는 matrix를 이용하게 되는데, 이것을 적용하면 된다. (선형대수학 개념)
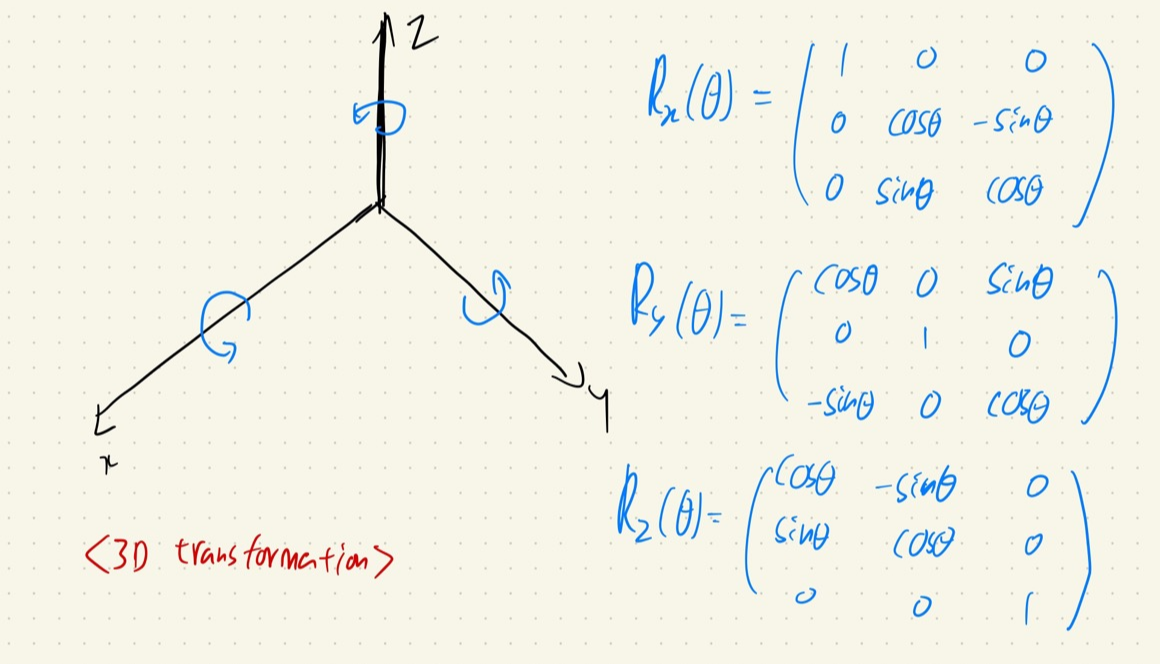
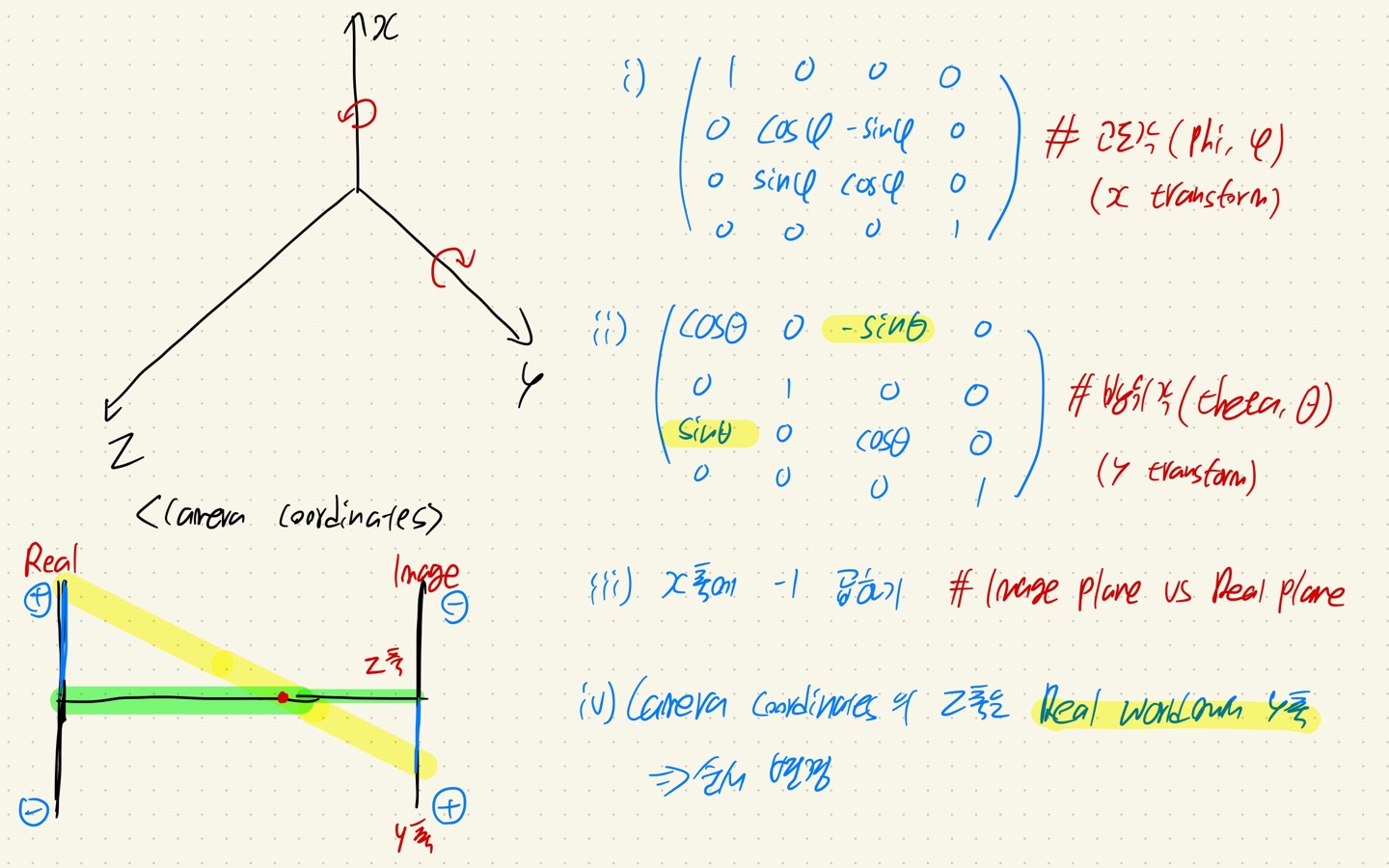
위의 사진을 보면, NeRF에서 3D transformation 하는 순서는 다음과 같다. (회전은 thumb rule을 따른다.)
- 1. phi(고도각)을 이용해서 X-axis를 rotation.
- 2. theta(방위각)을 이용해서 Y-axis를 rotation (기존 방향과 반대 방향으로 rotation)
- 3. X축의 부호 변경 (왜냐하면 Image plane에서 들어오면서 x축의 부호가 바뀌면서 들어온다)
- 4. Camera coordinates에서의 Z 축은 Real world에서의 Y축이다. 따라서, Camera coordinates의 행렬의 Y와 Z축의 위치를 변경해야 한다.
- 즉, Camera coordinates에서 Y축이 2행, Z 축이 3행이였다면, Real world에 적용시키기 위해서 Y축이 3행, Z축이 2행으로 변경시켜 준다.
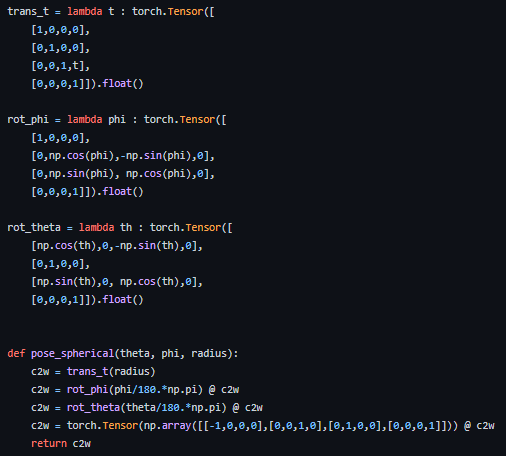
Code로 표현하면 위와 같이 표현할 수 있다.
여기서 못 보던, trans_t라는 항목이 있는데, 이것은 translation이라고 생각하면 된다.
즉, 우리가 카메라로 객체를 찍으면 반구(원형) 안에서 여러 각도에서 촬영하게 될 것인데, 카메라로부터 trans_t만큼 객체를 위치시킨다. 이 말은 Z 축 방향으로 trans_t만큼 이동한다는 뜻이 된다.
+) 또한 눈치가 빠르신 분들은, 3D transformation matrix가 3x3이 아니라 4x4로 이용되고 있다는 것을 확인하셨을 수도 있습니다.
이는 trans_t를 이용하기 위해서 기본적으로 3x4 행렬을 이용해야 하는데, 3x4 행렬의 경우 정사각행렬이 아니어서 나중에 역행렬을 계산할 수 없습니다 (선형대수학 개념)
따라서, 이것을 방지해주기 위해서 4차원의 한 점에 객체를 고정시켜 줍니다. (어떤 객체든 4차원의 고정된 위치에서 계산되므로 크게 의미가 없음)
즉, 4차원을 추가해서 4x4 정사각 행렬을 만들어주는 것입니다.
여기까지 Camera parameter에 대해서 설명을 해보았다.
코드와 같이 엮어서 설명했기 때문에 코드를 보고 이해할 때 좀 더 쉽게 할 수 있을 것이라고 생각이 든다.
다음으로는 NeRF의 핵심인 Ray를 설명해 보겠다.
Background Knowledge: Ray (directions)
NeRF는 기존의 Vision 분야와 다르게, batch 적용되는 데이터든, 기준이 pixel 단위이다. (NeRF는 좌표를 sampling 하여 이것을 학습시킨다. 이미지를 학습시키는 과정이 아니다!!)
이 점을 잘 생각해서 Ray를 이해해 보자.
1. Ray directions
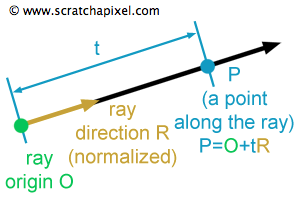
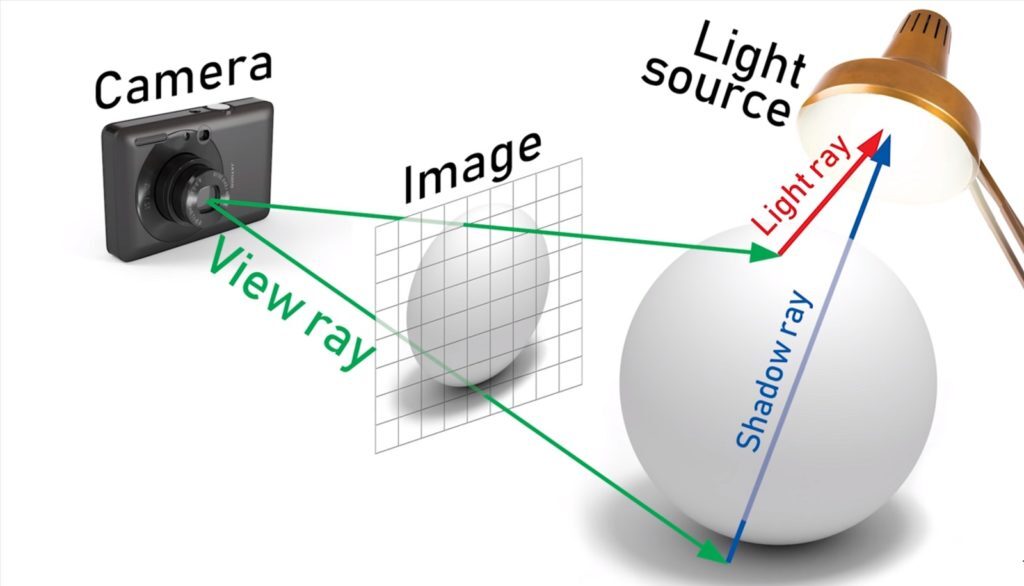
Ray는 이미지의 한 pixel 상에서 객체(3D)를 향해서 나아가는 방향벡터를 의미한다.
위의 사진을 보면, 카메라의 원점(초점; rays_o)과 카메라에서 객체를 향해서 나아가는 방향(direction; rays_d)이 Ray의 구성요소라고 할 수 있다.
즉 Ray를 표현하는 수식은 o + td가 된다. 여기서 t는 방향에 대한 가중치 정도이다. 즉 NeRF에서는 Z의 좌표 값이 t가 된다.
그리고 원점 o는 각 픽셀이 위치한 z 축 지점이 된다. (코드에서는 Normalized plane 기준에서 ray를 구하기 때문에 1이다.)
따라서, t = 0일 때, Z-axis의 값이 0이라는 의미이므로, 임의의 픽셀 좌표에서 객체를 향해서 나아가는 ray direciton 방향으로 z = 0이다.
만약 t = 10이라면, Z-axis의 값이 10이므로, 임의의 픽셀 좌표에서 rays_d(ray direction)의 방향으로 z = 10만큼 이동하게 될 것이다.
2. How to use Ray
이 Ray가 왜 중요하냐..!!
바로 NeRF의 목적이 이미지를 2D상에서 임의의 view에서 바라보았을 때, 그 이미지를 3D로 rendering로 시켜주는 것이기 때문에, 공간의 정보를 알아야 한다. 즉, 2D상에서 보이지 않는 Z-axis의 정보를 획득해야 한다는 말이 된다.
이를 표현하기 위해서, 카메라 원점에서 Ray를 발사해서, 객체를 통과하는 임의의 ray direction을 생성하고 그 ray direction 위에서 임의의 t값을 통해서 Z 좌표를 설정하여 학습을 하는 것이다.
천천히 위의 말을 사진과 함께 이해해 보자..!
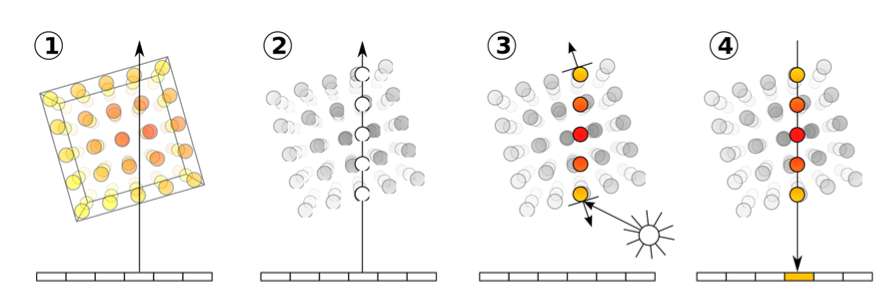
- 1. 한 이미지의 픽셀에서 객체를 통과하는 Ray를 발사한다.
- 2. Ray 위에서 임의의 지점에서 Z 축 좌표를 sampling 한다. 그러면 (x, y)에 대해서 여러 개의 z coordinates가 sampling 될 것이다. (논문에서는 64, 128을 이용한다. 밑에서 자세히 언급.)
- 3. Sampling 된 z 좌표마다 density와 RGB 값을 구한다. // (Density는 3D information이다. 객체의 투명도를 나타낸다고 생각하면 된다. 그리고 Density 값은 각 좌표에 대한 가중치로도 활용된다. (밑에서 자세히 언급.))
- 4. Density와 RGB값을 서로 곱한 후, 전부 더해서 (x, y)의 RGB를 계산한다.
이것이 NeRF의 메커니즘이자, Ray를 통해서 3D information 얻는 방법이다.
(x,y)의 RGB가 실제 Ground Truth의 RGB와 거의 유사하다면, Ray direciton 위에서 sampling 된 z 좌표들의 density 값과 rgb값이 거의 유사하다는 뜻이므로 이 정보를 이용해서 3D rendering을 할 수 있다.
여기서 한 가지 의문점이 생겨났을 수 있다.
Density는 무엇이고 왜 이것이 RGB를 계산할 때 가중치로 이용이 되는 것이지??
이 부분도 천천히 생각해 보자! (밑에 4번에 언급)
3. Calculate Rays

Ray는 앞에서 언급했던 Intrinsic parameter, C2W(Camera to World) matrix를 이용해서 계산이 된다.
- 첫 번째로, normalized plane의 (x, y)를 구하기 위해서 Image coordinate -> Normal plane과정을 진행한다. (위에서 Intrinsic parameter matrix로 focal length와 C를 이용하여 계산을 하는 과정이다.)
- 두 번째로, ray directions(rays_d)을 계산한다.
- 이 과정은, normalized plane에서 C2W matrix를 구해서 좌표계를 Real world로 변환시켜 준다.
- Shape은 (H, W, 3)으로 각각의 pixel에 대한 Ray가 담긴 행렬이 완성될 것이다.
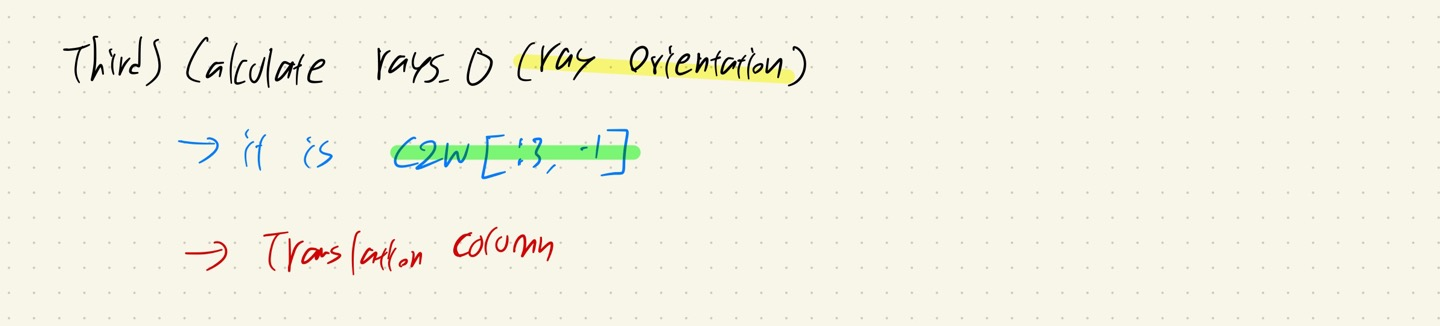
- 세 번째로, ray orientation(rays_o)을 계산한다.
- 이 과정은, C2W matrix의 translation을 담당했던 column이다.
- 가져온 후, shape을 rays_d와 동일하게 맞춰주기만 하면 된다.
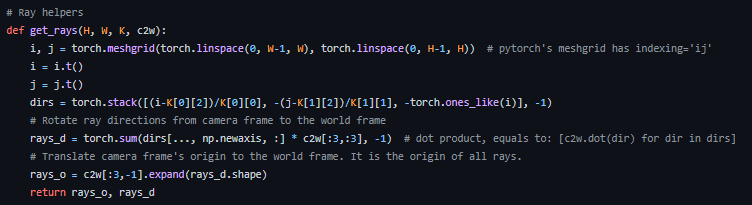
코드로 표현하면 위와 같다.
여기서 보이는 torch.meshgrid()는 Image plane의 coordinates를 가르쳐주는 변수이다.
여기서 주의할 점은, 위에서 언급했던 것처럼, Image plane은 아래로 갈수록 x가 증가한다는 것이다..!
+) 또한 dirs를 구하는 코드를 보면, 위와 수식 중에서 Y와 Z를 구하는 것이 약간 다를 것이다. stack 순서대로 [X, Y, Z]를 계산하는 것이다.
Y의 부호를 변경하는 이유는, Image plane에서 아래로 내려가면 Y의 값이 커지는데 Real world에서는 반대이다. (이미지 행렬 표현 방식을 생각하면 됨.)
Z의 부호를 변경하는 이유는, 초점을 기준으로, Normalized plane은 z = -1에 위치한다.
4. Density and RGB

위의 사진을 보면 Density가 무엇을 가리키는지 확실히 이해할 것이라고 생각한다.
말 그대로, 각 좌표들이 어느 정도의 밀도를 가지고 있는지 알려주는 것이다.
Density를 이용하는 이유는, 바로 객체의 불투명성에 있다.
배경을 둘러싸고 있는 공기들은 투명하기 때문에, 이미지 상의 RGB에 영향을 끼치지 못하고, Density도 낮을 것이다. 그러나 이미지에 있는 물건은 RGB에 직접적인 영향을 주고 Density도 높을 것이다.
바로 이러한 선형관계(?)를 떠올려서 Density를 이용해서 ray directions 위의 좌표들의 RGB 값에 곱해주고 전부 더해서 한 픽셀의 RGB 값을 결정짓는 것이다.
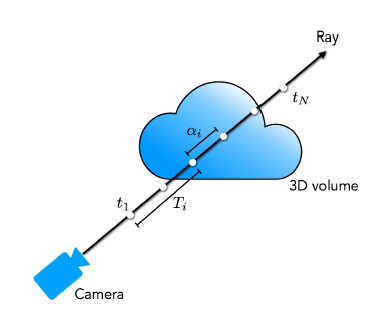
5. Volume Rendering
여기서 또 한가저 더 나아가서 생각해야 될 것이 있다.
z 좌표가 뒤에 있는 객체일수록, 픽셀의 RGB 값에 영향을 끼치지 못한다.
위의 구름 사진이 불투명하다고 가정해 보자.
그러면 구름 뒤에 사람이 있어도, 카메라가 바라보는 시점에서 사람의 RGB는 pixel에 영향을 주지 못할 것이다.
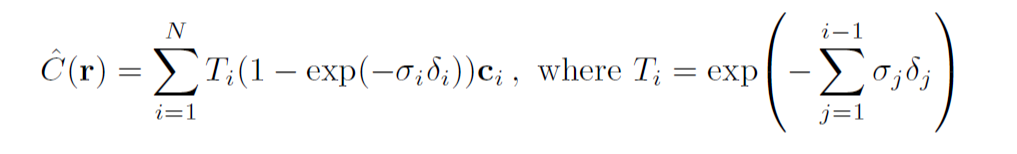
이를 모두 고려한 식이 바로 위의 식이 된다.
- Ti - density의 가중치 값
- σi - i번째의 density
- δi - ti-1과 ti사이의 거리 (위에서 언급되었던 z 좌표의 역할을 하는 t)
- Ci - i번째의 RGB 값
이 수식을 이용해서 각 (x, y)의 RGB값을 계산하게 됩니다. (위의 수식으로 rgb_map 생성)
T가 위에서 질문한 것에 대한 답변이 되는 가중치가 됩니다. 앞에 있는 객체들의 영향들을 고려해서, 뒤에 있는 객체가 아무리 불투명해도 RGB에 영향을 줄 수 없게 만듭니다.
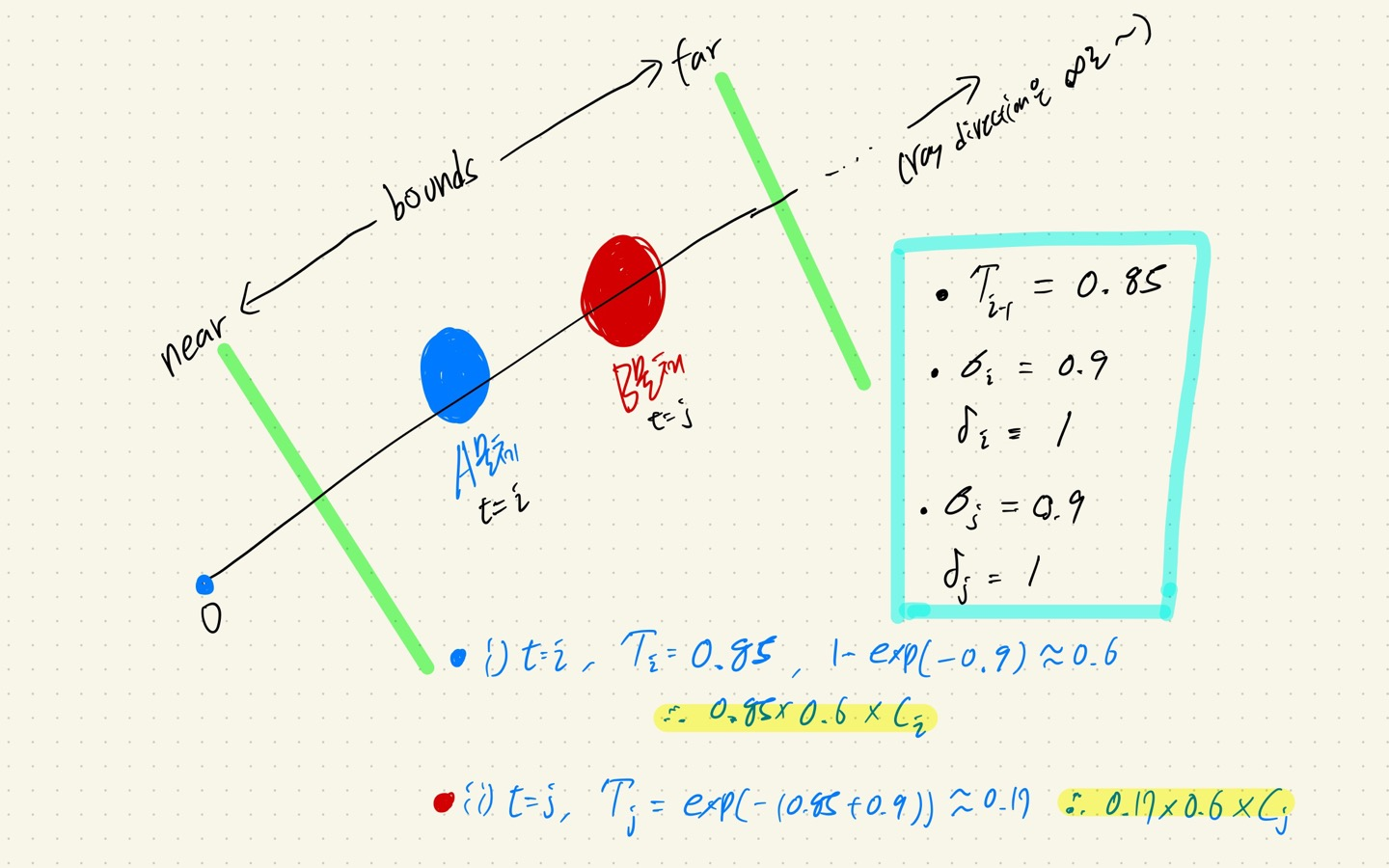
예시를 보면서 쉽게 이해해 봅시다!
A물체와 B물체가 있습니다. 둘 다 density가 0.9인 확실한(?) 객체들입니다.
이때, t=i 일 때, A물체의 RGB의 weights는 0.85 * 0.6입니다.
그러나 t=j 일 때, B물체 앞에 있는 A 물체의 density 영향으로 인해 Tj가 변하면서 가중치가 0.85에서 0.17로 줄어듭니다. 최종적으로 B물체의 RGB의 weights는 0.17 * 0.6입니다.
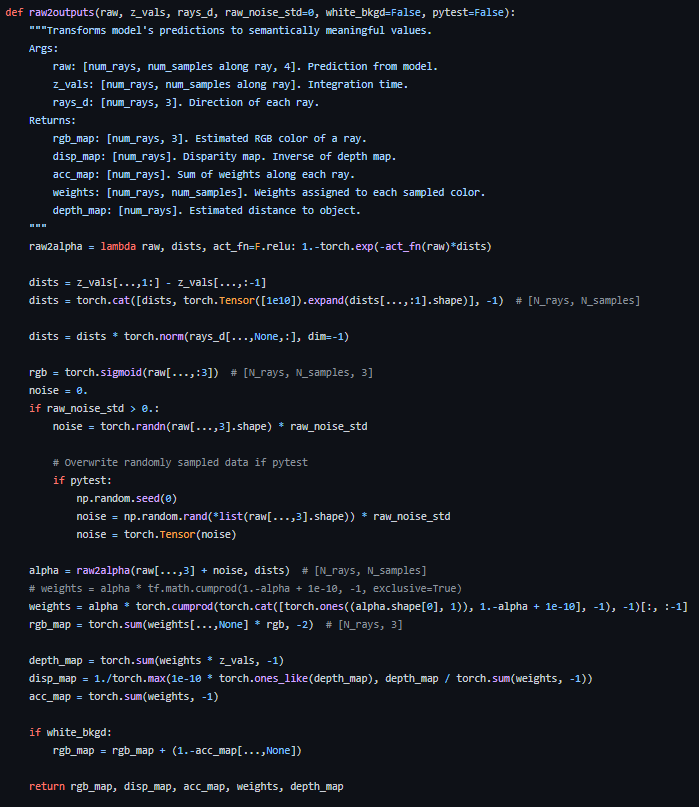
코드로 보면 이 부분에 해당합니다!
여기서 여러 가지고 트릭이 있습니다.
- 1. alpha(1-exp(-σδ))를 구할 때, density값에 음수가 있을 수도 있기 때문에 ReLU를 적용합니다.
- 2. dists는 sampling 된 좌표 간의 거리를 나타내는데, 일단 (1부터~end지점), (0부터~끝지점) 이렇게 좌표 행렬을 만든 후 서로 빼줍니다. 그리고 dists의 마지막 원소에 1e10을 넣는데, 마지막 거리는 사실상 거의 무한대로 본다고 판단합니다.
- 3. RGB의 음수값이 있을 수도 있기 때문에 sigmoid를 적용합니다. (나중에 255를 곱하는 연산이 있습니다.)
- 4. T의 첫 번째 값은 무조건 1이어야 하기 때문에, T에 1을 넣어서 concat을 한 후 마지막 값을 뺀 상태로 계산합니다.
- 5. disp_map을 만들 때 depth_map(density 값)이 0일 수도 있어서 작은 값 1e-10과 max() 연산을 합니다.
+) 추가적으로, Ray에 보면 near와 far라는 value가 있습니다. 이것은 NeRF를 implementation 할 때도 볼 수 있는 옵션입다.
이 항목은 Ray direction에서 나오는 z 좌표의 값들은 사실상 무한대까지 생성이 가능합니다.
근데, 이 범위를 제한해주기 위해서, 가장 가까운 z 좌표를 near, 가장 먼 z 좌표를 far라고 설정하고 그 안에서 z 좌표들을 sampling 하게 됩니다.
여기까지 Ray부터 시작해서 volume rendering을 알아보았습니다.
마지막 스텝으로, Model 구조와 훈련 네트워크를 살펴봅시다!
NeRF: Model structure
드디어 NeRF의 모델 구조와 어떻게 학습하는지 한번 알아보자.
위의 내용들을 잘 상기하면서 읽으면 이해하는데 큰 도움이 될 것이다!
1. NeRF Overview
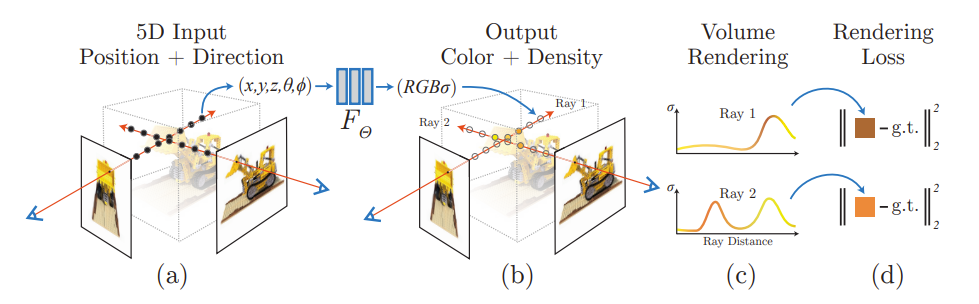
NeRF의 간략한 Overview라고 할 수 있는 논문의 사진이다.
첫 번째는 NeRF는 5D input이다.
NeRF는 사진에 보는 것처럼 (x, y, z, θ, ϕ)를 input으로 넣어준다. (θ: theta, ϕ:phi)
이 5개 값이 그대로 학습에 이용되는 것은 아니다.
(θ, ϕ)는 extrinsic parameters인 C2W를 만들 때 이용이 되고, C2W를 통해서 만들어진 각 (x, y)의 Ray와 Ray 위에서 sampling 되는 z가 model의 input으로 들어간다. 즉 모델의 처음 들어가는 실질적인 input은 (x, y, z)인 것이다.
또한 NeRF는 모델 중간에 Ray의 view directions을 넣어준다. (밑에 모델 구조에서 자세히)
두 번째는 NeRF의 output은 4-dimension이다.
NeRF는 output dimension으로 [RGB, Density]를 결괏값으로 내보낸다. 여기서 RGB는 3차원, Density는 1차원이다.
* 학습 데이터의 이미지의 shape도 (N, H, W, 4)이다.
세 번째는 NeRF는 각 pixel의 예측된 RGB값과 ground-truth의 RGB 값 사이의 MSE loss를 통하여서 backpropagation을 진행한다.
이제 좀 더 자세히 들어가 보자!
2. Model structure: MLP
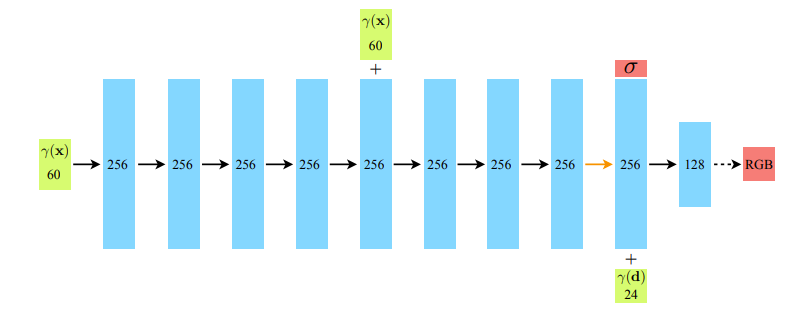
NeRF의 모델 구조는 MLP로 구성되어 있다.
여기서 처음 input이 분명 (x, y, z)라고 했는데 어떻게 γ(x)가 60-dimension 인지 궁금할 것이다.
또한 모델의 마지막에 들어가는 γ(d)는 view directions인데 24-dimenstion이다..!!
이는 바로 Positional embedding 방법을 이용한 것이다.
2-1. Positional embedding
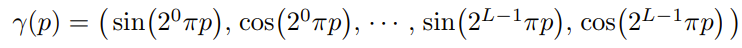
논문에서 소개하고 있는 Positional embedding 방법이다.
수식만 보고 바로 적용되기가 어려울 것이다.
여기서 중요한 값은 L이다.
(x, y, z)에서는 L=10으로 설정하여서, x,y,z를 각각 20차원(L=10일 때, sin, cos이 2번씩 10번 적용되므로)으로 늘려서 총 60차원이 되고,
view directions을 구성하고 있는 (x,y,z)에서는 L=4을 적용하여서 총 24차원이 되는 것이다.
(* view directions은 Ray인데, Ray는 앞에서 언급했던 것처럼, 각 (x, y)에 대한 ray의 방향 값, 즉 z값을 가지고 있다.)
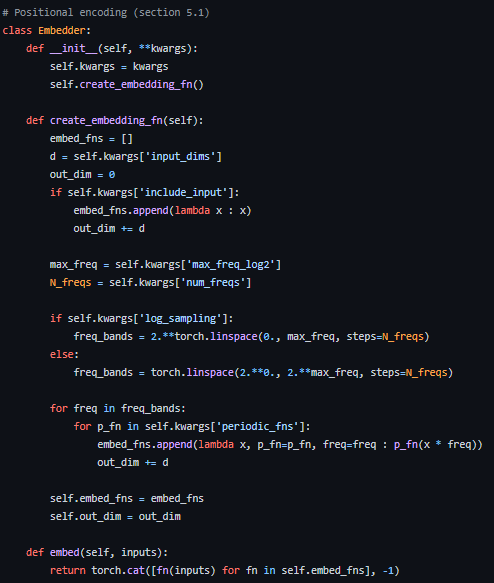
추가적으로, code에 보면 self.kwargs ['include_input']이라는 옵션이 있는데, 이것을 적용하면 기존의 (x, y, z) 좌표를 같이 활용해서 63차원, 27차원으로 변한다.
성능 면에서도 기존 (x, y, z)의 coordinate를 합해서 학습하는 것이 더 좋다.
2-2. Model output
Model의 구조를 보면 중간에 density가 나오고, 다시 view directions이 들어가고 마지막에는 RGB layer가 나온다.
하지만 그림만으로 정확히 언제 어디서 density가 나오는지 파악하기 힘들다.
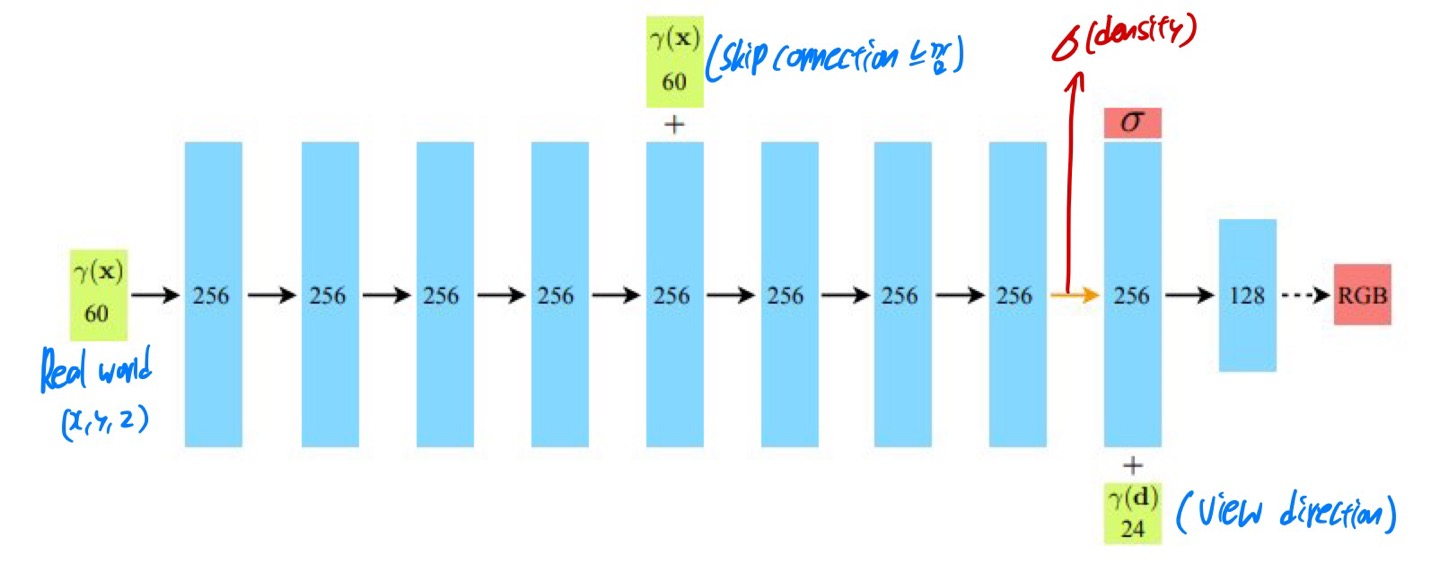
위의 사진을 보면, density는 view directions이 들어가기 전에 output으로 나오고, 이후에 view directions이 layer에 합쳐진다.
이 점을 주의해야 한다!!
여기서 view directions이 (x, y, z)로 이루어져 있고, input으로 들어가는 (x, y, z)도 Ray에서 sampling 된 것인데, 둘이 어떠한 차이점이 있는지 궁금한 점을 느끼시는 분들이 있을 것 같다.
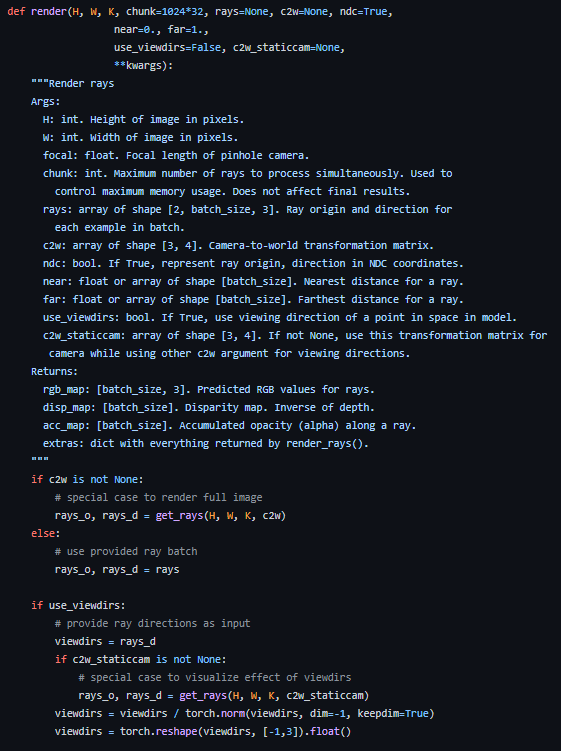
차이점을 명확하게 알려면, 코드를 봐야 한다..!!!
- 1. (x, y, z)를 계산하는 rays_d(ray directions) 값은 real world에 대한 ray directions으로, (x,y,z) coordinates는 Real world에 해당하는 sampling 좌표들이다.
- 2. View directions은 rays_d로 일단 할당받고, 방향에 대한 크기가 각 좌표마다 다르지 않고, 방향만 고려될 수 있도록 normalization을 해준 것이다. 따라서 각 (x, y)에 해당하는 ray direction의 크기가 1인 행렬이 되는 것이다.
2-3. Model network
위에서 끝이었으면 좋겠지만, 아직 조금 더 남았다!
NeRF는 똑같은 구조를 가진 network가 2개가 있는데, 2개를 동시에 학습하는 구조를 가진다.
두 개의 network가 무엇이 다른지 한번 살펴보자!
2-3-1. Coarse Network

Coarse network는 일단 가장 기본적인 NeRF이다.
위의 봤던 volume rendering 수식과 똑같다! 한 가지 다른 점은, 여기서 계산된 값은 실제 rendering 할 때 이용되지 않는다.
풀어서 설명하면, Stratified sampling을 이용하여 Nc개의 점에 대해서 먼저 계산이 이루어진다.
그리고 Nc점에 대한 각각의 wi를 구한다. 즉 sampling 된 Nc 점에 대한 가중치 행렬을 가지고 Fine network로 간다.
* Stratified sampling은 코드에서 단순하게 torch.rand로 이루어진다.
* 코드에서 Coarse Network에서의 samplin 개수는 64개, Fine network에서는 128개를 이용한다.
2-3-2. Fine Network

Fine network에서는 Coarse network에서 구한 wi를 normalizing을 한 후, Ray에 대한 PDF(확률밀도함수)를 구한다. 그 후에 CDF(누적분포함수)를 가지고 inverse-transform-sampling을 통해서 Nf개를 sampling 한 후, Nc+Nf를 새로운 NeRF에 input으로 넣어서 학습시킨다.
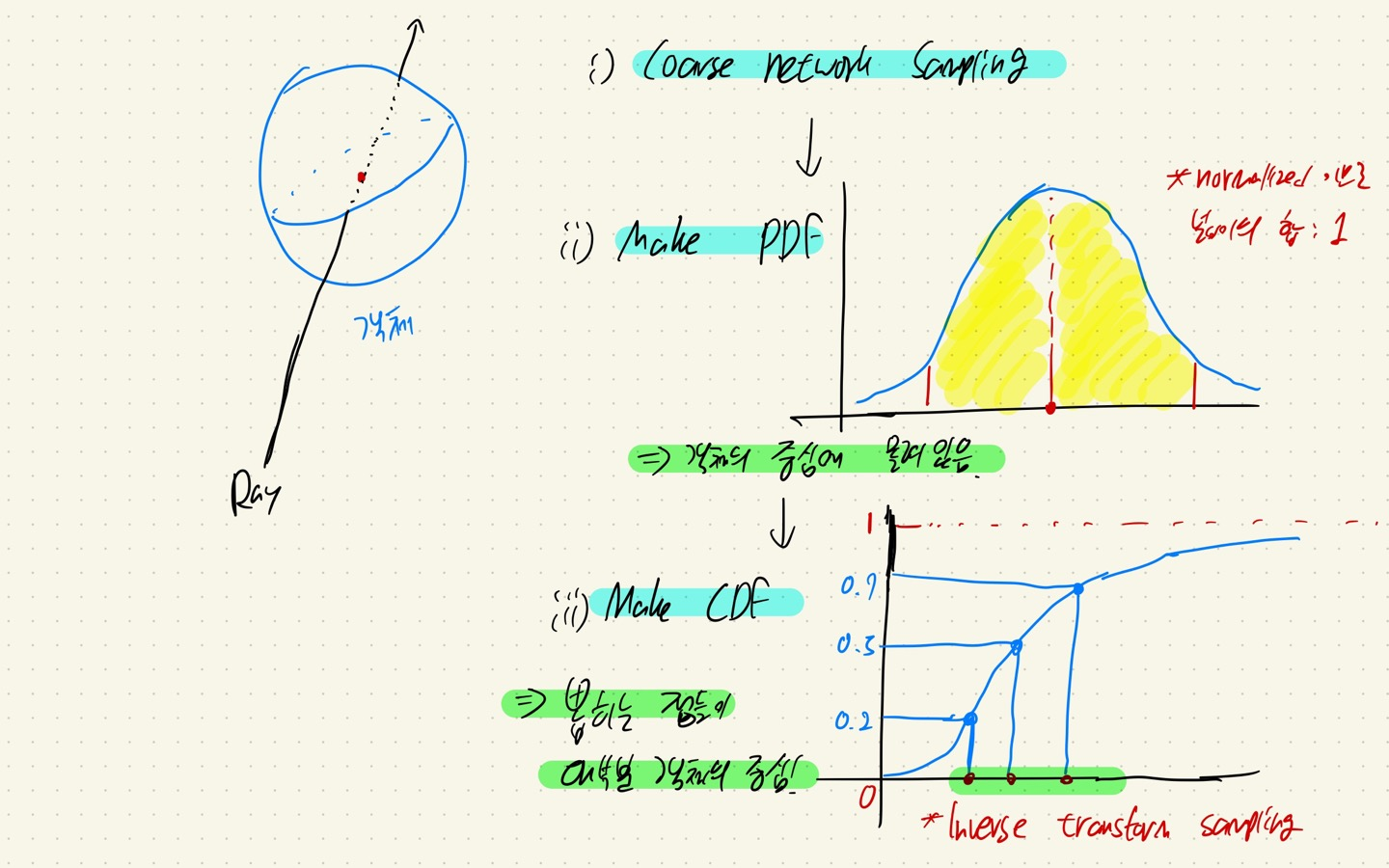
이 말이 무슨 뜻이냐!
- 1. Coarse network에서 Sampling을 진행한다.
- 2. Coarse network에서 나온 좌표들로 PDF를 구성하는데, normalizing을 통해서 적분 값이 1이 되도록 한다.
- 3. PDF를 통해서 CDF를 만든다.
- 4. CDF에서 Inverse transform sampling을 통해서 Nf개를 추출한다.
- y는 0~1 사이로 이루어져 있는데, 여기서 랜덤 하게 y값을 고른 후, x로 Inverse transform 시키면 대부분 객체의 중앙에 위치한 z 좌표들이 sampling 된다.
- 이것을 통해서, 객체의 중심부를 좀 더 잘 표현할 수 있다.
2-3-3. Model loss function
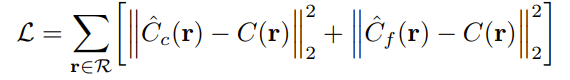
Model은 위에서 언급했던 것처럼, RGB 값에 대한 차이를 가지고 mse를 계산하는데, Cc와 Cf에 대한 각각의 network loss function을 계산하게 된다.
여기서 주의해야 할 점은, 여기서 계산되는 RGB는 0~1 사이 값을, 위에서 sigmoid를 적용한 상태이다!
여기까지 Model의 구조와 Training을 하는 방법에 대해서 알아보았다..!!
지금까지의 Ray를 만드는 과정은 Blender 데이터를 기준으로 이루어졌다.
마지막으로 real data인 llff를 다룰 때 사용되는 옵션인 Normalized Device Coordinate를 알아보고 끝내도록 하겠다. (+blender vs llff의 비교까지)
Normalized Device Coordinate
NDC(Normalized Device Coordinate)라고 불리는 이것은 공간 스펙트럼에 대한 모양을 normalized 시켜주는 것이다.
이것을 설명하기 전에 dataset에 대해서 한번 간단히 얘기를 하고 가겠다!
Blender dataset은 NeRF에서 많이 보이는 데이터셋인데, 가장 큰 특징은 배경이 전부 흰색이라는 것이다.
즉, 가상의 환경에서 만들어진 데이터로 Camera parameter를 별도의 연산과정 없이 바로 얻을 수 있으며 자유로운 각도의 view direction에서의 이미지를 얻을 수 있고, 거의 360도 방향으로 데이터셋을 구성할 수 있다.
반면 llff dataset은 real scene데이터로 실제 데이터셋이다.
이는 Blender dataset과는 다르게 각도가 한정되어 있는 forward facing scene이고, 대부분 앞쪽에서 찍힌 이미지고 사진에 대한 camera parameter 정보가 없어서 직접 구해야 하는 단점이 있다.
우리가 지금까지 다뤘던 ray의 계산 방식은 Blender dataset이다. 물론 이 방법을 llff처럼 real scene data에 적용해도 되지만 NDC를 적용한 ray를 이용하면 더 성능이 올라간다.
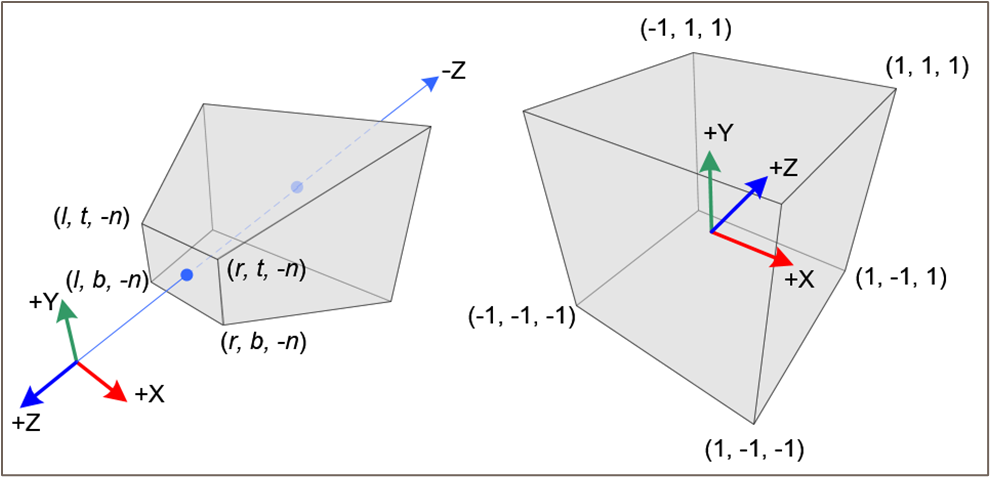
위의 사진을 보면, 왼쪽은 기존의 ray이다.
기존의 ray의 모양은 사다리꼴 모양으로 되어 있는 육면체를 구성하고 있다.
하지만 이럴 경우,. 공간에 대한 좌표의 입력값이 불규칙할 수 있고 공간 표현에 있어서 효율적이지 못하다.
따라서 공간의 좌표를 [-1, 1]로 projection 시키는 방법이 NDC이다!! 이럴 경우 공간의 모양은 정육면체로 구성이 된다.
우리는 기존의 ray를 projection 시켜줄 matrix를 구해야 한다.
이 방법을 잘 소개한 블로그가 있어서 사진으로 설명을 대체하겠다..!

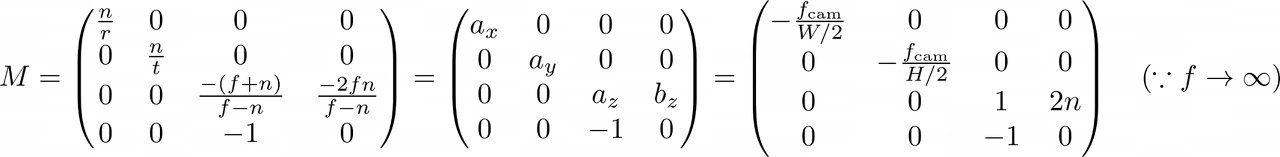
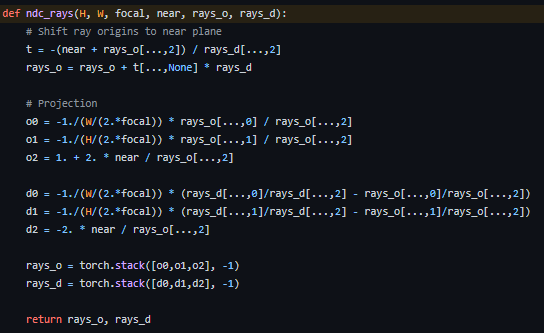
실제 NeRF 코드에서도 위와 같이 NDC를 적용할 수 있게 코드를 구성했으니, forward-facing형태의 dataset이면 NDC를 적극적으로 활용하도록 하자..!
긴 글 읽어주셔서 너무나 감사하고,
나중에 시간되면 코드 설명과 함께 github 공유해보도록 하겠습니다..!
질문있으면 댓글로 남겨주시면 제가 아는 범위 내에서 성실하게 답변드리겠습니다.
감사합니다!!
- 2022.12.23. 학부생 3학년인 kyujinpy 작성
이미지 출처(자세한 이미지 번호는 추후 기재): https://www.youtube.com/watch?v=zkeh7Tt9tYQ



