*LoRA를 위한 논문 리뷰 글입니다! 궁금하신 점은 댓글로 남겨주세요!
LoRA paper: https://arxiv.org/abs/2106.09685
LoRA: Low-Rank Adaptation of Large Language Models
An important paradigm of natural language processing consists of large-scale pre-training on general domain data and adaptation to particular tasks or domains. As we pre-train larger models, full fine-tuning, which retrains all model parameters, becomes le
arxiv.org
LoRA github: https://github.com/microsoft/LoRA
GitHub - microsoft/LoRA: Code for loralib, an implementation of "LoRA: Low-Rank Adaptation of Large Language Models"
Code for loralib, an implementation of "LoRA: Low-Rank Adaptation of Large Language Models" - GitHub - microsoft/LoRA: Code for loralib, an implementation of "LoRA: Low-Rank Adaptati...
github.com
Contents
- LoRA(Low-Rank-Parameterized Updated Matrices)
Simple Introduction

최근 chatGPT 열풍에 이어 LLM에 대한 인기가 매우 뜨겁다.
여기서 문제점으로 언급된 것이 fine-tuning할 때 모델의 파라미터가 너무 많다보니 리소스 제약이 크다는 점이였다.
오늘 소개할 LoRA 논문은 기존의 파라미터보다 훨씬 적은 파라미터를 가지고 튜닝하는 방법으로 통해서 리소스 제약에서 벗어나고 성능도 비슷하거나 더 높은 수준으로 훈련시킬 수 있도록 하는 수학적인 메커니즘을 소개하고 있다.
Method
Introduction

LoRA의 overview 이미지이다.
매우 간단해보이지만, 너무나 획기적인 방법이라고 할 수 있다.
이 이미지에서 볼 수 있는 것처럼, 기존의 weights 대신 새로운 파라미터를 이용해서 동일한 성능과 더 적은 파라미터로 튜닝할 수 있는 방법론을 제시하고 있다.

먼저 Wq, Wk, Wv, Wo는 각각 query/key/value/output을 의미한다.
또한 W와 W0는 pretrained weight이고 ΔW는 adapation을 할 때 축적되는 기울기 업데이트에 대한 값이라고 생각하면 된다.


본격적인 설명에 앞서서 문제 정의와 용어를 정리하고 넘어가겠다.
1. 기존의 LLM모델(예를 들어 GPT)를 하나의 확률함수 PΦ(y|x)라고 하겠다. (여기서 y와 x는 context-target pair쌍이라고 생각하면 편함.)
2. 그리고 fine-tuning과정에서 LLM이 튜닝되는 Φ가 최적화 되는 식은 equation1처럼 표현 될 수 있다.
- Log-likelihood function으로 문제를 해결할 때 가장 적합한 파라미터 Φ의 나올 확률을 최대화 하는 것이라고 생각하면 된다.
- 직관적으로 backpropagation할 때의 모델을 나타내면, Φ = Φ0 + ΔΦ 이렇게 된다.
3. Eqaution1에 근거하여 만약 accmulated gradient values(ΔΦ)를 기존보다 훨씬 적은 파라미터인 Θ로 치환하여 ΔΦ(Θ)로 나타내면 equation2로 바뀌게 된다.
- 즉 기존의 log-likelihood 문제에서 모델이 backpropagation 과정에서 이용되는 파라미터 연산문제를 더 적은 파라미터 Θ로 치환하여 풀겠다는 의미이다.
이제 본격적으로 LoRA를 설명해보겠다!
LoRA(Low-Rank-Parameterized Update Matrices)

LoRA(Low-Rank Adaptation)는 매우 간단하다!
1. Pre-trained weight matrix W0가 (d,k) dimension이라고 하자.
2. 그리고 accmulated gradient values(ΔW) 또한 (d,k) dimension을 최종적으로 가지게 될 텐데, 이것을 row-rank r을 이용해서 ΔW = BA로 나타낸다. (B는 (d,r), A는 (r,k) dimension을 가진다.)
- 또한 r은 min(d,k)보다 작도록 정의된다.
3. 훈련과정에서 W0는 gradient update를 하지 않고, 오히려 BA를 학습하는 과정으로 이루어진다.
4. 즉 forward passing 과정을 표현하면 equation 3와 같다.
+) 추가적으로 A는 random gaussian initialization으로 시작하고, B는 0으로 시작하여 BA의 초깃값은 0이다.

+) ΔW를 a/r로 scaling한다는 표현이 있어서 코드를 살펴보았는데, result에다가 그대로 scaling해서 값을 보내는 형태였다. (a는 임의의 값.)

+) Transformer에 LoRA를 적용할 때는 Wq, Wk, Wv, Wo 중 몇개를 훈련시킨다.
Result
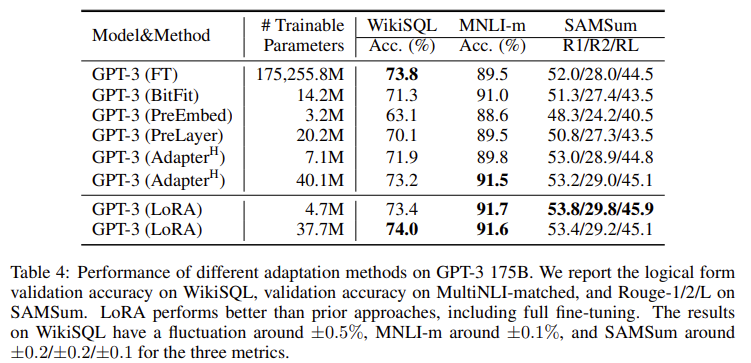
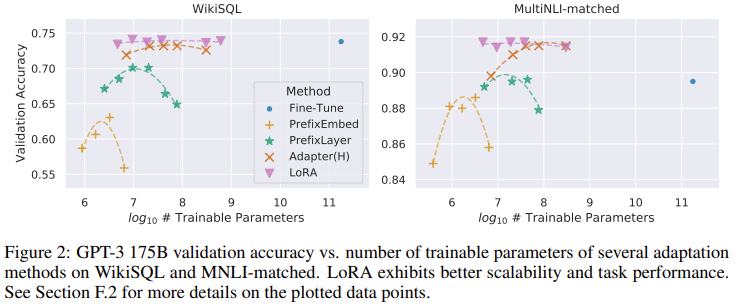
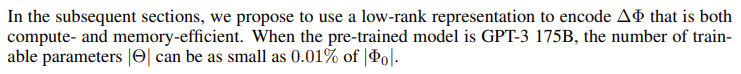
- LoRA를 이용하였을 때 해당 fields에서 SOTA를 달성할 뿐만 아니라, GPT-3의 경우 175B의 파라미터 가운데 0.01%의 파라미터 개수만 이용할 정도로 효율성이 좋다.
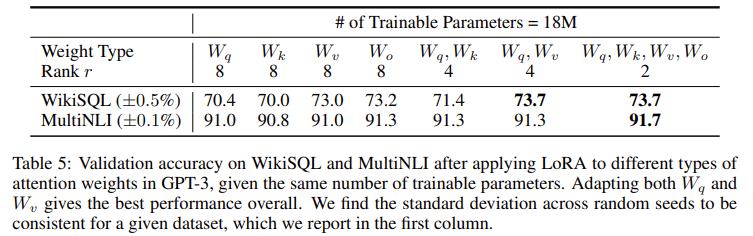
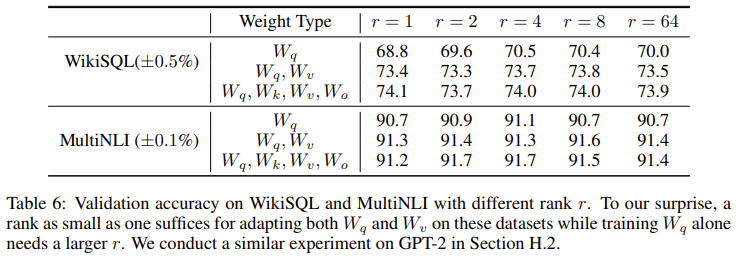
- 또한 LoRA에서 r=1일 때 꽤 좋은 성능이 나온다는 것을 볼 수 있다.

- 논문의 저자들이 r=8일 때와 r=64일 때 모델을 pre-training 시키면서 ΔWq와 ΔWv의 subspace 유사도를 계산해본 자료이다.
- 논문의 말이 어렵게 느껴질 수도 있는데, r=8이면 subspace dimension이 8까지 있다고 생각하면 r=8일 때와 r=64일 때의 나오는 각각의 8개의 subspace와 64개의 subspace간의 전부 similarity를 계산한 것이다.
- r=8일 때와 r=64일 때를 보면 subspace의 dimension중 1일 때 similairty가 0.5보다 크다는 것을 확인할 수 있다.
- 이것을 바탕으로 low-adaption rank(r)=1일 때도 성능이 좋다고 생각할 수 있다.
Furthermore
QLoRA: [2305.14314] QLoRA: Efficient Finetuning of Quantized LLMs (arxiv.org)
QLoRA: Efficient Finetuning of Quantized LLMs
We present QLoRA, an efficient finetuning approach that reduces memory usage enough to finetune a 65B parameter model on a single 48GB GPU while preserving full 16-bit finetuning task performance. QLoRA backpropagates gradients through a frozen, 4-bit quan
arxiv.org
QLoRA 논문리뷰: [미정]
LoRA를 재미있게 읽었다면 LoRA를 발전시킨 QLoRA도 읽어보기를 추천한다!
- 2023.07.01 Kyujinpy 작성.
(다시 본격적으로 논문리뷰 시작..?)



