*DDPM을 이해하셔야 읽기 편하실 것 같습니다..!
Study Github: https://github.com/KyujinHan/DDPM-study
GitHub - KyujinHan/DDPM-study: Denoising Diffusion Probabilistic Models code study
Denoising Diffusion Probabilistic Models code study - GitHub - KyujinHan/DDPM-study: Denoising Diffusion Probabilistic Models code study
github.com
DDPM github: https://github.com/lucidrains/denoising-diffusion-pytorch
GitHub - lucidrains/denoising-diffusion-pytorch: Implementation of Denoising Diffusion Probabilistic Model in Pytorch
Implementation of Denoising Diffusion Probabilistic Model in Pytorch - GitHub - lucidrains/denoising-diffusion-pytorch: Implementation of Denoising Diffusion Probabilistic Model in Pytorch
github.com
DDPM 간단한 코드 예제
from denoising_diffusion_pytorch import Unet, GaussianDiffusion, Trainer
model = Unet(
dim = 64,
dim_mults = (1, 2, 4, 8),
flash_attn = True
)
diffusion = GaussianDiffusion(
model,
image_size = 128,
timesteps = 1000, # number of steps
sampling_timesteps = 250 # number of sampling timesteps (using ddim for faster inference [see citation for ddim paper])
)
trainer = Trainer(
diffusion,
'path/to/your/images',
train_batch_size = 32,
train_lr = 8e-5,
train_num_steps = 700000, # total training steps
gradient_accumulate_every = 2, # gradient accumulation steps
ema_decay = 0.995, # exponential moving average decay
amp = True, # turn on mixed precision
calculate_fid = True # whether to calculate fid during training
)
trainer.train()DDPM의 코드는 간단하게 이루어 진다!
Unet(model)을 정의 -> GaussianDiffusion 정의 -> Trainer 정의 후 훈련!
하지만 이렇게 아는 것은 deep하게 diffusion의 수식을 코드에 적용하여 확인하지 못한다.
한번 더 깊게 들어가서 살펴보자!!
Unet 코드
# Unet class
class Unet(nn.Module):
def __init__(
self,
dim,
init_dim = None,
out_dim = None,
dim_mults = (1, 2, 4, 8),
channels = 3,
self_condition = False,
resnet_block_groups = 8,
learned_variance = False,
learned_sinusoidal_cond = False,
random_fourier_features = False,
learned_sinusoidal_dim = 16,
sinusoidal_pos_emb_theta = 10000,
attn_dim_head = 32,
attn_heads = 4,
full_attn = None, # defaults to full attention only for inner most layer
flash_attn = False
):
super().__init__()
##################### determine dimensions
self.channels = channels
self.self_condition = self_condition
input_channels = channels * (2 if self_condition else 1)
init_dim = default(init_dim, dim) # init_dim과 dim 중에 선택
'''
def default(val, d):
if exists(val):
return val
return d() if callable(d) else d
'''
self.init_conv = nn.Conv2d(input_channels, init_dim, 7, padding = 3)
dims = [init_dim, *map(lambda m: dim * m, dim_mults)]
in_out = list(zip(dims[:-1], dims[1:]))
##################### resnetBlock에 time embedding이 들어간다
block_klass = partial(ResnetBlock, groups = resnet_block_groups) # resnet Block 정의
(...이후 생략...)Unet Class이다!
간단하게 위와 같이 정의되는데, 코드를 전부 살펴보는 것은 직접(?) 해보길 바라고, 중요한 코드 라인만 짚고 넘어가보겠다!
##################### resnetBlock에 time embedding이 들어간다
block_klass = partial(ResnetBlock, groups = resnet_block_groups) # resnet Block 정의
## 참고: ResetnetBlock class
### -> time_embedding이 들어간다는 사실!
class ResnetBlock(nn.Module):
def __init__(self, dim, dim_out, *, time_emb_dim = None, groups = 8):
super().__init__()
self.mlp = nn.Sequential(
nn.SiLU(),
nn.Linear(time_emb_dim, dim_out * 2)
) if exists(time_emb_dim) else None
self.block1 = Block(dim, dim_out, groups = groups) # 아래에 정의
self.block2 = Block(dim_out, dim_out, groups = groups)
self.res_conv = nn.Conv2d(dim, dim_out, 1) if dim != dim_out else nn.Identity()
def forward(self, x, time_emb = None):
scale_shift = None
if exists(self.mlp) and exists(time_emb):
time_emb = self.mlp(time_emb)
time_emb = rearrange(time_emb, 'b c -> b c 1 1')
scale_shift = time_emb.chunk(2, dim = 1)
h = self.block1(x, scale_shift = scale_shift)
h = self.block2(h)
return h + self.res_conv(x)
################# Time embedding 방법
sinu_pos_emb = SinusoidalPosEmb(dim, theta = sinusoidal_pos_emb_theta)
fourier_dim = dim
## time mlp -> 임베딩 값과 비슷한 느낌
self.time_mlp = nn.Sequential(
sinu_pos_emb,
nn.Linear(fourier_dim, time_dim),
nn.GELU(),
nn.Linear(time_dim, time_dim)
)
## 참고: SinusoidalPosEmb class
class SinusoidalPosEmb(nn.Module):
def __init__(self, dim, theta = 10000):
super().__init__()
self.dim = dim
self.theta = theta
def forward(self, x):
device = x.device
half_dim = self.dim // 2
emb = math.log(self.theta) / (half_dim - 1)
emb = torch.exp(torch.arange(half_dim, device=device) * -emb)
emb = x[:, None] * emb[None, :]
emb = torch.cat((emb.sin(), emb.cos()), dim=-1)
return emb-> ResetNet code
-> Time embedding이 들어간다는 것을 기억하자!
-> 일단 t값은 time_mlp layer를 통과하게 된다. 따라서 SinusoidalPosEmb -> linear -> GELU -> Linear의 형태를 걸쳐서 time embeddlng이 만들어 진다.
#################### attention 연산
if not full_attn:
full_attn = (*((False,) * (len(dim_mults) - 1)), True)
num_stages = len(dim_mults)
full_attn = cast_tuple(full_attn, num_stages)
attn_heads = cast_tuple(attn_heads, num_stages)
attn_dim_head = cast_tuple(attn_dim_head, num_stages)
assert len(full_attn) == len(dim_mults)
FullAttention = partial(Attention, flash = flash_attn) # Attention 정의
## 침고1: Attention class
class Attention(nn.Module):
def __init__(
self,
dim,
heads = 4,
dim_head = 32,
num_mem_kv = 4,
flash = False
):
super().__init__()
self.heads = heads
hidden_dim = dim_head * heads
self.norm = RMSNorm(dim)
self.attend = Attend(flash = flash) # 아래에 정의
self.mem_kv = nn.Parameter(torch.randn(2, heads, num_mem_kv, dim_head))
self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, bias = False)
self.to_out = nn.Conv2d(hidden_dim, dim, 1)
def forward(self, x):
b, c, h, w = x.shape
x = self.norm(x)
qkv = self.to_qkv(x).chunk(3, dim = 1) # output 3개
q, k, v = map(lambda t: rearrange(t, 'b (h c) x y -> b h (x y) c', h = self.heads), qkv)
mk, mv = map(lambda t: repeat(t, 'h n d -> b h n d', b = b), self.mem_kv) # random parameters
k, v = map(partial(torch.cat, dim = -2), ((mk, k), (mv, v)))
out = self.attend(q, k, v)
out = rearrange(out, 'b h (x y) d -> b (h d) x y', x = h, y = w)
return self.to_out(out)
## 참고2: Attend class (Flash attention 여기서 구현함.)
class Attend(nn.Module):
def __init__(
self,
dropout = 0.,
flash = False
):
super().__init__()
self.dropout = dropout
self.attn_dropout = nn.Dropout(dropout)
self.flash = flash
assert not (flash and version.parse(torch.__version__) < version.parse('2.0.0')), 'in order to use flash attention, you must be using pytorch 2.0 or above'
# determine efficient attention configs for cuda and cpu
self.cpu_config = AttentionConfig(True, True, True)
self.cuda_config = None
if not torch.cuda.is_available() or not flash:
return
device_properties = torch.cuda.get_device_properties(torch.device('cuda'))
if device_properties.major == 8 and device_properties.minor == 0:
print_once('A100 GPU detected, using flash attention if input tensor is on cuda')
self.cuda_config = AttentionConfig(True, False, False)
else:
print_once('Non-A100 GPU detected, using math or mem efficient attention if input tensor is on cuda')
self.cuda_config = AttentionConfig(False, True, True)
def flash_attn(self, q, k, v):
_, heads, q_len, _, k_len, is_cuda, device = *q.shape, k.shape[-2], q.is_cuda, q.device
q, k, v = map(lambda t: t.contiguous(), (q, k, v))
# Check if there is a compatible device for flash attention
config = self.cuda_config if is_cuda else self.cpu_config
# pytorch 2.0 flash attn: q, k, v, mask, dropout, causal, softmax_scale
with torch.backends.cuda.sdp_kernel(**config._asdict()):
out = F.scaled_dot_product_attention(
q, k, v,
dropout_p = self.dropout if self.training else 0.
)
return out
def forward(self, q, k, v):
"""
einstein notation
b - batch
h - heads
n, i, j - sequence length (base sequence length, source, target)
d - feature dimension
"""
q_len, k_len, device = q.shape[-2], k.shape[-2], q.device
if self.flash:
return self.flash_attn(q, k, v)
scale = q.shape[-1] ** -0.5
# similarity
sim = einsum(f"b h i d, b h j d -> b h i j", q, k) * scale
# attention
attn = sim.softmax(dim = -1)
attn = self.attn_dropout(attn)
# aggregate values
out = einsum(f"b h i j, b h j d -> b h i d", attn, v)
return out-> Attention code
-> Flash attention을 이용할 수 있는 옵션이 있다! 이것말고는 attention 연산과 똑같다고 생각하면 된다.
################# layers
self.downs = nn.ModuleList([])
self.ups = nn.ModuleList([])
num_resolutions = len(in_out)
for ind, ((dim_in, dim_out), layer_full_attn, layer_attn_heads, layer_attn_dim_head) in enumerate(zip(in_out, full_attn, attn_heads, attn_dim_head)):
is_last = ind >= (num_resolutions - 1)
attn_klass = FullAttention if layer_full_attn else LinearAttention
self.downs.append(nn.ModuleList([
block_klass(dim_in, dim_in, time_emb_dim = time_dim),
block_klass(dim_in, dim_in, time_emb_dim = time_dim),
attn_klass(dim_in, dim_head = layer_attn_dim_head, heads = layer_attn_heads),
Downsample(dim_in, dim_out) if not is_last else nn.Conv2d(dim_in, dim_out, 3, padding = 1)
]))
mid_dim = dims[-1]
self.mid_block1 = block_klass(mid_dim, mid_dim, time_emb_dim = time_dim)
self.mid_attn = FullAttention(mid_dim, heads = attn_heads[-1], dim_head = attn_dim_head[-1])
self.mid_block2 = block_klass(mid_dim, mid_dim, time_emb_dim = time_dim)
for ind, ((dim_in, dim_out), layer_full_attn, layer_attn_heads, layer_attn_dim_head) in enumerate(zip(*map(reversed, (in_out, full_attn, attn_heads, attn_dim_head)))):
is_last = ind == (len(in_out) - 1)
attn_klass = FullAttention if layer_full_attn else LinearAttention
self.ups.append(nn.ModuleList([
block_klass(dim_out + dim_in, dim_out, time_emb_dim = time_dim),
block_klass(dim_out + dim_in, dim_out, time_emb_dim = time_dim),
attn_klass(dim_out, dim_head = layer_attn_dim_head, heads = layer_attn_heads),
Upsample(dim_out, dim_in) if not is_last else nn.Conv2d(dim_out, dim_in, 3, padding = 1)
]))
default_out_dim = channels * (1 if not learned_variance else 2)
self.out_dim = default(out_dim, default_out_dim)
self.final_res_block = block_klass(dim * 2, dim, time_emb_dim = time_dim)
self.final_conv = nn.Conv2d(dim, self.out_dim, 1)-> Reverse process layer
-> Down-sampling -> Mid block -> Up-sampling
################## Unet forward 과정
## 여기서 x는 이미지 형태의 차원
## time은 단일 값 (gaussian diffusion 코드에서 더 자세히)
def forward(self, x, time, x_self_cond = None):
assert all([divisible_by(d, self.downsample_factor) for d in x.shape[-2:]]), f'your input dimensions {x.shape[-2:]} need to be divisible by {self.downsample_factor}, given the unet'
if self.self_condition: # False
x_self_cond = default(x_self_cond, lambda: torch.zeros_like(x))
x = torch.cat((x_self_cond, x), dim = 1)
x = self.init_conv(x)
r = x.clone()
t = self.time_mlp(time) # t step에 관련된 t-value
h = []
for block1, block2, attn, downsample in self.downs:
x = block1(x, t)
h.append(x)
x = block2(x, t)
x = attn(x) + x
h.append(x)
x = downsample(x)
x = self.mid_block1(x, t)
x = self.mid_attn(x) + x
x = self.mid_block2(x, t)
for block1, block2, attn, upsample in self.ups:
x = torch.cat((x, h.pop()), dim = 1) # skip connection
x = block1(x, t)
x = torch.cat((x, h.pop()), dim = 1)
x = block2(x, t)
x = attn(x) + x
x = upsample(x)
x = torch.cat((x, r), dim = 1) # r = x = self.init_conv(x)
x = self.final_res_block(x, t)
return self.final_conv(x)-> Unet Forward 과정
-> DDPM에서의 reverse process에 해당하는 파라미터 값

Unet의 layer는 우리가 DDPM 논문에서 수식과 이론으로 엄청 공부했던(?)
reverse process의 파라미터 값이라고 생각하면 편하다.
위의 수식에서 eta_theta 값에 해당한다!
이제 안에 들어가는 평균, 표준편차, t값에 대한 정의는 아래의 Gaussian Diffusion코드에서 살펴보도록 하자!
GaussianDiffusion 코드
########## GaussianDiffusion code 생략
class GaussianDiffusion(nn.Module):
def __init__(
self,
model,
*,
image_size,
timesteps = 1000,
sampling_timesteps = None,
objective = 'pred_v',
beta_schedule = 'sigmoid',
schedule_fn_kwargs = dict(),
ddim_sampling_eta = 0.,
auto_normalize = True,
offset_noise_strength = 0., # https://www.crosslabs.org/blog/diffusion-with-offset-noise
min_snr_loss_weight = False, # https://arxiv.org/abs/2303.09556
min_snr_gamma = 5
):
super().__init__()
assert not (type(self) == GaussianDiffusion and model.channels != model.out_dim)
assert not model.random_or_learned_sinusoidal_cond
self.model = model
self.channels = self.model.channels
self.self_condition = self.model.self_condition
self.image_size = image_size
self.objective = objective
assert objective in {'pred_noise', 'pred_x0', 'pred_v'}, 'objective must be either pred_noise (predict noise) or pred_x0 (predict image start) or pred_v (predict v [v-parameterization as defined in appendix D of progressive distillation paper, used in imagen-video successfully])'
(...이후 생략...)GaussianDiffusion class이다!
여기에는 너무나 중요한 부분들이 있는데 코드로 한번 살펴보겠다.
######################## beta scheduler-> sigmoid
## DDPM은 학습에 이용되는 beta_t의 값을 constant하게 유지하기 때문에
if beta_schedule == 'linear':
beta_schedule_fn = linear_beta_schedule
elif beta_schedule == 'cosine':
beta_schedule_fn = cosine_beta_schedule
elif beta_schedule == 'sigmoid':
beta_schedule_fn = sigmoid_beta_schedule
else:
raise ValueError(f'unknown beta schedule {beta_schedule}')
# timesteps = 1000
# -> steos = 1001
betas = beta_schedule_fn(timesteps, **schedule_fn_kwargs)
## 참고: sigmoid_beta_schedule
def sigmoid_beta_schedule(timesteps, start = -3, end = 3, tau = 1, clamp_min = 1e-5):
"""
sigmoid schedule
proposed in https://arxiv.org/abs/2212.11972 - Figure 8
better for images > 64x64, when used during training
"""
steps = timesteps + 1
t = torch.linspace(0, timesteps, steps, dtype = torch.float64) / timesteps
v_start = torch.tensor(start / tau).sigmoid()
v_end = torch.tensor(end / tau).sigmoid()
alphas_cumprod = (-((t * (end - start) + start) / tau).sigmoid() + v_end) / (v_end - v_start)
alphas_cumprod = alphas_cumprod / alphas_cumprod[0]
betas = 1 - (alphas_cumprod[1:] / alphas_cumprod[:-1])
return torch.clip(betas, 0, 0.999)-> Beta schedule
-> DDPM 논문에서는 beta 값을 constant하게 유지한다.
-> 그리고 beta의 특성상 b1이 가장 작고, b_T가 가장 커야 한다.
-> 바로 이것을 조절해주는 것이 sigmoid_beta_schedule(default 값) 이다.
######################### 논문 정의
## alpha를 통하여서, 빠른 전개가 가능하도록 함.
alphas = 1. - betas
alphas_cumprod = torch.cumprod(alphas, dim=0) # t개만큼의 누적곱
alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value = 1.)
########################-> alpha define
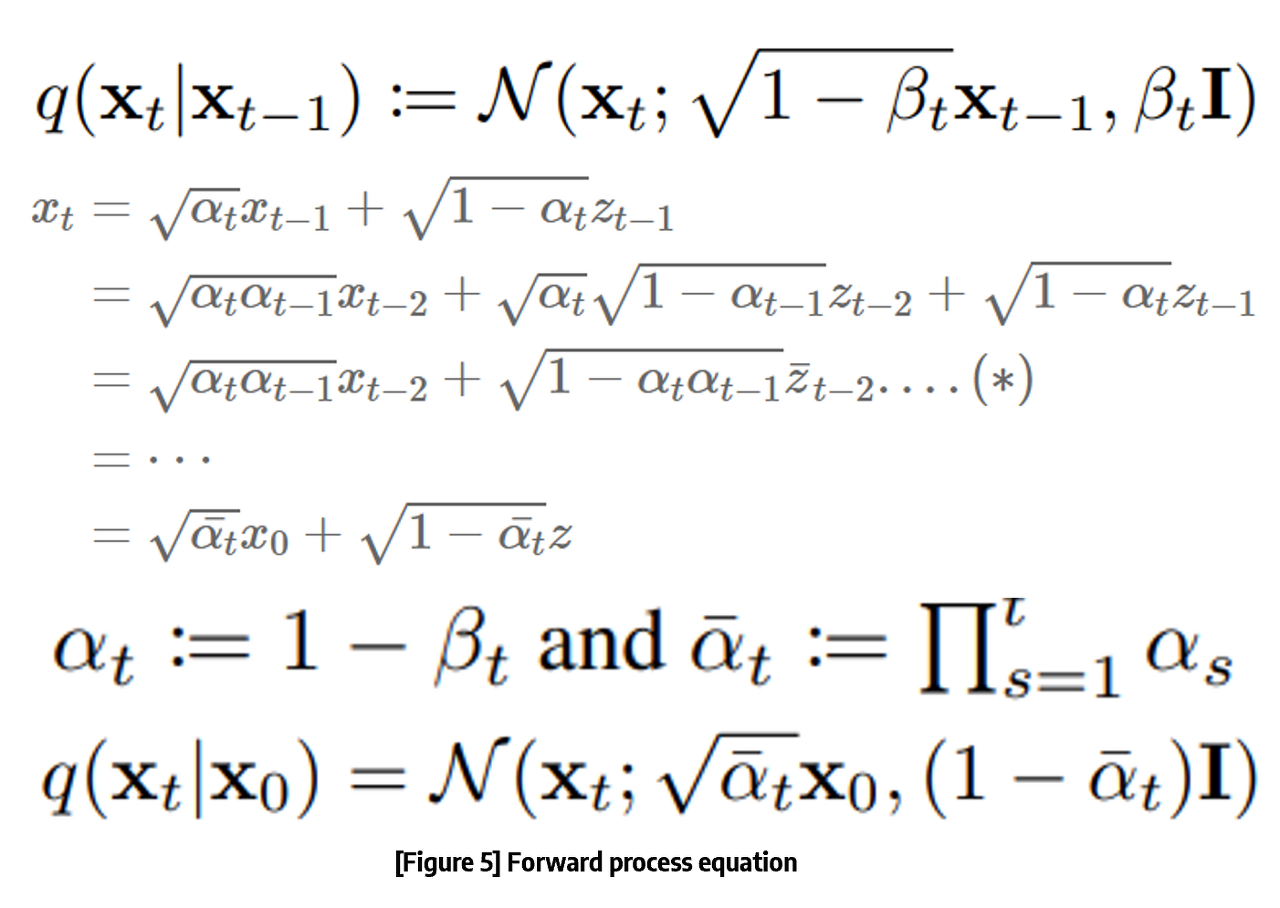
-> alpha는 Diffusion process에서 너무나도~~ 중요한 존재이다.
-> alpha를 통해서 q(Xt|X0)의 수식이 X0로 표현 가능해졌기 때문이다!!
######################## 논문에서 이용되는 수식 정의
assert self.sampling_timesteps <= timesteps
self.is_ddim_sampling = self.sampling_timesteps < timesteps # ddim 목록 (나중에)
self.ddim_sampling_eta = ddim_sampling_eta # ddim 목록 (나중에)
# helper function to register buffer from float64 to float32
## register_buffer를 써야하는 이유: https://www.ai-bio.info/pytorch-register-buffer
### register_buffer에 등록된 애들은 자동으로 cuda로 옮기기 편하다.
#### register_buffer에 등록된 애들은 학습 되지 않는다! (아주 중요!!)
register_buffer = lambda name, val: self.register_buffer(name, val.to(torch.float32))
register_buffer('betas', betas)
register_buffer('alphas_cumprod', alphas_cumprod)
register_buffer('alphas_cumprod_prev', alphas_cumprod_prev)
# calculations for diffusion q(x_t | x_{t-1}) and others
register_buffer('sqrt_alphas_cumprod', torch.sqrt(alphas_cumprod)) # forward process의 q(Xt|X0)
register_buffer('sqrt_one_minus_alphas_cumprod', torch.sqrt(1. - alphas_cumprod)) # forward process의 q(Xt|X0)
register_buffer('log_one_minus_alphas_cumprod', torch.log(1. - alphas_cumprod))
register_buffer('sqrt_recip_alphas_cumprod', torch.sqrt(1. / alphas_cumprod))
register_buffer('sqrt_recipm1_alphas_cumprod', torch.sqrt(1. / alphas_cumprod - 1))
# calculations for posterior q(x_{t-1} | x_t, x_0)
## 논문에서는 간단하게 beta_t를 분산으로 쓰는 것도 제안함
posterior_variance = betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod)
# above: equal to 1. / (1. / (1. - alpha_cumprod_tm1) + alpha_t / beta_t)
register_buffer('posterior_variance', posterior_variance)
# below: log calculation clipped because the posterior variance is 0 at the beginning of the diffusion chain
register_buffer('posterior_log_variance_clipped', torch.log(posterior_variance.clamp(min =1e-20)))
register_buffer('posterior_mean_coef1', betas * torch.sqrt(alphas_cumprod_prev) / (1. - alphas_cumprod))
register_buffer('posterior_mean_coef2', (1. - alphas_cumprod_prev) * torch.sqrt(alphas) / (1. - alphas_cumprod))
#########################-> equation define (important)
-> register_buffer를 활용한 DDPM에서 이용되는 수식을 정의한다.
-> 여기 있는 값들은 학습에 이용되지 않는다! (당연)

-> 여기서 다시, DDPM의 분산 정의를 짚고 넘어가보자..!
-> register_buffer를 통해서, alphas_cumprod를 정의하고, 그것을 바탕으로 평균과, 표준편차에 이용되는 값들을 정의하고, posterior_variance를 통해서 분산도 정의한다.
########################## derive loss weight
# snr - signal noise ratio
## Check: 언제 사용될까? 좀 지켜보기
### -> loss * self.loss_weight
snr = alphas_cumprod / (1 - alphas_cumprod)
# https://arxiv.org/abs/2303.09556
maybe_clipped_snr = snr.clone()
if min_snr_loss_weight:
maybe_clipped_snr.clamp_(max = min_snr_gamma) # min_snr_gamma
# default: pred_v
if objective == 'pred_noise': # 기존의 DDPM: noise 예측
register_buffer('loss_weight', maybe_clipped_snr / snr)
elif objective == 'pred_x0': # x0를 예측하는 것
register_buffer('loss_weight', maybe_clipped_snr)
## velocity v
#### https://arxiv.org/abs/2112.10752
##### Check: 더 살펴보기
elif objective == 'pred_v':
register_buffer('loss_weight', maybe_clipped_snr / (snr + 1))-> target type (important)
-> DDPM의 loss를 계산할 때, target값을 무엇으로 할지 정하는 코드이다.
-> 기존 논문에서는 eta(noise)값을 예측하는 방향으로 수식을 설계했는데 다른 관점도 있었다.
-> x0의 값을 예측하는 방법, velocity V를 예측하는 방법
-> default 값은 velocity V를 예측하는 방법이었는데, 아래에서 V가 무엇인지 살펴보겠다.
--> 추가적으로 t값에 따라 loss_weight를 설정하는 부분이 있다. 해당 부분은 signal noise ratio를 이용하여 설정하게 되는데, 아래에 어떻게 이용되는지 설명이 나와있다 (SNR관련 자료: https://ko.wikipedia.org/wiki/%EC%8B%A0%ED%98%B8_%EB%8C%80_%EC%9E%A1%EC%9D%8C%EB%B9%84#)
####### forward!!
def forward(self, img, *args, **kwargs):
b, c, h, w, device, img_size, = *img.shape, img.device, self.image_size
assert h == img_size and w == img_size, f'height and width of image must be {img_size}'
t = torch.randint(0, self.num_timesteps, (b,), device=device).long() # num_timesteps: 1000 // b: size (batch size)
# t를 무작정 1~1000까지 다 생성하는게 아니고,
### 이미지 하나당 무작위 수의 t를 하나씩 매핑해서, 그 t에 맞는 random noise를 생성한 후, loss 계산 (중요!!)
img = self.normalize(img) # norm
return self.p_losses(img, t, *args, **kwargs) # p_losses-> Gaussian Diffusion forward
-> image의 batch size만큼 t를 추출한다. (t가 단일 값;)
-> 그 이후 t값을 이미지와 함께 reverse process에 넣는다.
############################## reverse process
def p_losses(self, x_start, t, noise = None, offset_noise_strength = None):
b, c, h, w = x_start.shape
noise = default(noise, lambda: torch.randn_like(x_start)) # randn_like -> 정규분포 따름 (diffusion process이므로 당연!)
###### offset noise - https://www.crosslabs.org/blog/diffusion-with-offset-noise
offset_noise_strength = default(offset_noise_strength, self.offset_noise_strength)
if offset_noise_strength > 0.:
offset_noise = torch.randn(x_start.shape[:2], device = self.device)
noise += offset_noise_strength * rearrange(offset_noise, 'b c -> b c 1 1')
######
####### noise sample
x = self.q_sample(x_start = x_start, t = t, noise = noise) # diffusion process
#######
#######
# if doing self-conditioning, 50% of the time, predict x_start from current set of times
# and condition with unet with that
# this technique will slow down training by 25%, but seems to lower FID significantly
x_self_cond = None
if self.self_condition and random() < 0.5: ### self_condition 나중에 살펴보기 // unet에서 정의할 때는 False
with torch.inference_mode():
x_self_cond = self.model_predictions(x, t).pred_x_start
x_self_cond.detach_()
#######
######## predict and take gradient step
## model에 넣기 -> unet + attention
model_out = self.model(x, t, x_self_cond)
if self.objective == 'pred_noise':
target = noise
elif self.objective == 'pred_x0':
target = x_start
elif self.objective == 'pred_v': #################### what is it?
v = self.predict_v(x_start, t, noise)
target = v
else:
raise ValueError(f'unknown objective {self.objective}')
#######
####### loss 계산
loss = F.mse_loss(model_out, target, reduction = 'none')
loss = reduce(loss, 'b ... -> b', 'mean')
loss = loss * extract(self.loss_weight, t, loss.shape) ## self.loss_weight -> 각 t번째 마다 각각 다른 weight를 할당함.
return loss.mean # batch의 평균
#######
## 참고: q_sample
def q_sample(self, x_start, t, noise = None):
noise = default(noise, lambda: torch.randn_like(x_start))
return (
extract(self.sqrt_alphas_cumprod, t, x_start.shape) * x_start + # alphas_cumprod = torch.cumprod(alphas, dim=0) # t개만큼의 누적곱
extract(self.sqrt_one_minus_alphas_cumprod, t, x_start.shape) * noise # torch.sqrt(1. - alphas_cumprod)
) ## (평균*x0 + 표준편차*eta) # eta ~ N(0,1) ==> Diffusino 논문에서 소개하는 q(Xt | X0) 수식
'''
def extract(a, t, x_shape):
b, *_ = t.shape # batch size
out = a.gather(-1, t) # 여러 alpha 값 중에서
return out.reshape(b, *((1,) * (len(x_shape) - 1)))
'''
### 참고: predict_v
def predict_v(self, x_start, t, noise):
return (
extract(self.sqrt_alphas_cumprod, t, x_start.shape) * noise -
extract(self.sqrt_one_minus_alphas_cumprod, t, x_start.shape) * x_start
)-> p_losses 함수 (important)
-> 일단 q_sample 함수를 통해서 x를 출력한다.

-> 위의 수식이 q_sample 함수이다. (복습!!)
-> 그리고 난 이후, q_sample에 만들어진 x_t값과 t값의 Unet에 넣어서 output 출력한다.
-> model_objective가 pred_v이므로 predict_v 함수로 가서 target value를 정한다.
-> predict_v에서의 수식을 보면 velocty V가 어떻게 정의되는지 알 수 있다.
-> DDPM loss 수식대로 mse로 계산한다.
--> 마지막에 loss_weight를 곱해서 t에 따른 loss 가중치를 부여한다.
@torch.inference_mode()
def p_sample(self, x, t: int, x_self_cond = None):
b, *_, device = *x.shape, self.device
batched_times = torch.full((b,), t, device = device, dtype = torch.long)
model_mean, _, model_log_variance, x_start = self.p_mean_variance(x = x, t = batched_times, x_self_cond = x_self_cond, clip_denoised = True)
noise = torch.randn_like(x) if t > 0 else 0. # no noise if t == 0
pred_img = model_mean + (0.5 * model_log_variance).exp() * noise
return pred_img, x_start
@torch.inference_mode()
def p_sample_loop(self, shape, return_all_timesteps = False):
batch, device = shape[0], self.device
img = torch.randn(shape, device = device)
imgs = [img]
x_start = None
for t in tqdm(reversed(range(0, self.num_timesteps)), desc = 'sampling loop time step', total = self.num_timesteps):
self_cond = x_start if self.self_condition else None
img, x_start = self.p_sample(img, t, self_cond)
imgs.append(img)
ret = img if not return_all_timesteps else torch.stack(imgs, dim = 1)
ret = self.unnormalize(ret)
return ret-> DDPM sampling code
2023.12.30 kyujinpy 작성,
- 다음에는 DDIM 코드 리뷰로!
- non-makrovian chain 구현(?)
'AI > CV project' 카테고리의 다른 글
| [DiT-3D or DDPM Code 분석] (0) | 2024.09.24 |
|---|---|
| [SMPL-X Implementation] KyujinHan/Smplify-X-Perfect-Implementation (30) | 2024.03.18 |
| [Tune-A-VideKO] - 한국어 기반 One-shot Tuning of diffusion for Text-to-Video 모델 (0) | 2023.08.18 |
| [KO-stable-diffusion-anything] - 한국어 기반의 stable-diffusion-disney와 KO-anything-v4-5 (0) | 2023.08.16 |
| [OpenFlaminKO] - Polyglot-KO를 활용한 한국어 기반 MultiModal 도전기! (0) | 2023.08.16 |



