*Topology (위상수학)에 대해서 정리한 글입니다.
*두서가 없을 수도 있고, 위상수학을 복습한다는 마음으로 정리했습니다!
*입문하시는 분들께 도움이 되었으면..ㅎㅎ
Contents
- Pasting Lemma
- Constructing continuous functions
- Homeomorphism funny example
- Metric
- Diameter
- Standard bounded metric & Uniform metric
- Euclidean metric and Square metric are the same in product topology R^n
- Uniformly Converges
Continuous

위상수학의 꽃에 도달하기 직전(?) 마주치는 아름다운 개념! 연속(Continous)이다.
연속성을 거리개념없이 증명할 수 있다는 사실이 매우 놀랍지 않은가!?
Continous의 위상적 정의는
- X에서 Y로 보내는 function F가 있다고 하자. 이때 Y의 open subset A가 있다고 가정하자. 만약 A를 역함수 f를 통해서 매핑된 subset B (in X)가 X에서 open이라면 f는 continuous하다!

Continous의 동치 개념은 총 3가지가 있다.
function을 f라고 가정하자.
0) A in Y is open, then f^(-1)(A) is open in X.
1) Let A is subset in X, then f(Cl(A)) in Cl(f(A)).
2) A is closed set in Y, then f^(-1)(A) is closed in X. (Important)
3) Let each x in X, and each nhbd V of f(x). Then there is a nhbd U of x, such that f(U) in V.
위의 응용 중에서 특히 2번은 너무나 잘 활용된다!
(증명도 해보시면 도움이 됩니다!)

혹여나 continous의 동치개념 중 nhbd를 활용한 개념이 이해가 되지 않은 분들은 위의 이미지를 참고해보세요!
Homeomorphism

Homeomorphism의 정의는
- f가 bijective이고, f와 f^(-1)이 continous라면, f는 homemorphism이다
Pasting lemma
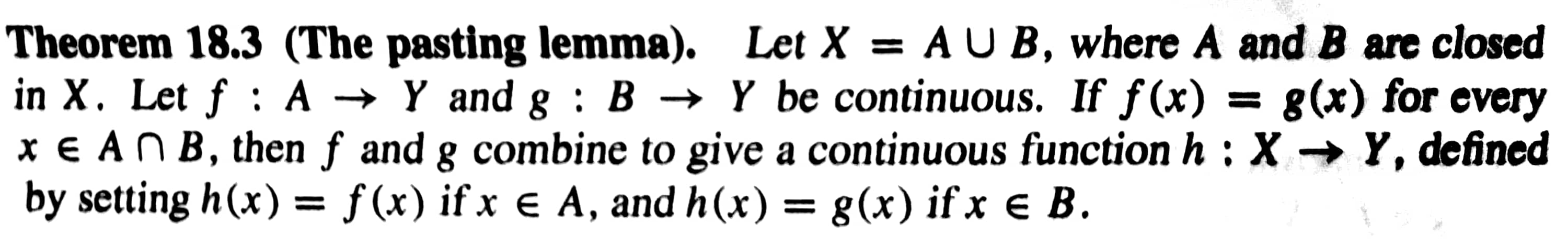
Pasting lemma는 너무나 쉽다!
- A와 B가 closed set이라고 가정하고, f는 X->Y인 continuous라고 하자. 그렇다면 A와 B의 교집합인 x가 f(x)=g(x)라면 f(x)와 g(x)를 서로 pasting(연결)한 function h(x) continuous이다!

Pasting lemma를 시각화하면 위와 같다!
Constructing contnuous functions

Continuous function의 정의로 우리가 흔히 아는(?) 함수의 연속성 정리를 다시 위상적으로 표현한 것이다.
정말 여러가지가 있지만 이 중에서 3개는 너무나 중요하다!
1) Constant function is continuous
2) Inclusion is continuous (즉 X의 subset A에서 X로 보내는 것도 continous)
3) Composites is continuous
Homeomorphism funny example

f:X->Y가 있을 때,
f가 continuous하고 bijective하다고 가정하자.
우리가 배우기로는 f의 역함수도 continous해야하지만, 위상적인 관점에서는 무조건 그렇지 않다!
따라서 f가 homemorphism하지 않는데, 위의 예제를 보면 이해가 될 것이다!
Metric topology
Metric

Topology를 처음 소개할 때, 거리라는 개념이 없다고 소개했다!
근데 `거리` 개념과 거의 유사한(?) metric이 등장한다!
Metric topology는 정말 감사하다.. 너무 편하다 ㅎㅎ
편하게 생각한다면 metric ball, 즉 임의의 epsilon>0을 가지는 open set을 떠올리면 편하다!
특히 metric topology에서는 triangle inequality가 매우 중요하다! (topology 정리4에서 다루겠습니다!)

Diameter

diameter는 임의의 집합 a1, a2에 있는 2개의 점 사이에서 가장 supremum인 것을 고르는 것이다!
(여기서 왜 maxmimum이 아니라 supremum일까요? 해석학을 들었다면 당연히 알아야할 사실!)
Standard bounded metric & Uniform metric

Standard bounded topology는 기존의 정의된 metric d(x,y)와 1을 비교하여 minimum인 값을 고르는 것이다!

Uniform metric 이다!
해당 metrix은 function 간의 비교를 할 때 쓰인다!
*(점들 간의 비교가 아닌 function들의 metric!!!)
(이것들이 왜 필요할까? 나중에 connectedness와 compactness를 metric topology에서 보일 때 자주 사용한다!)
Euclidean metric and Square metric are the same in product topology R^n

Euclidean space R^n에서 만들어지는 metric topologies (sqaure, euclidean)들은 서로 같다라는 증명이다!
흥미로워서 소개합니다!
Uniformly Converges

Function의 sequence fn을 설정한다고 했을 때,
n이 무한에 가까워질 때 그 수렴하는 정도가 균일하다면 converges uniformly라고 한다.

아주 좋은 시각화 이미지가 있어서 가져와 봤다.
f(x)가 있을 때, fn(x)가 uniformly converges하다는 말은, 모든 x에 대해서 f와 fn의 차이가 임의의 eplison>0 보다 작아야 된다는 의미이다!
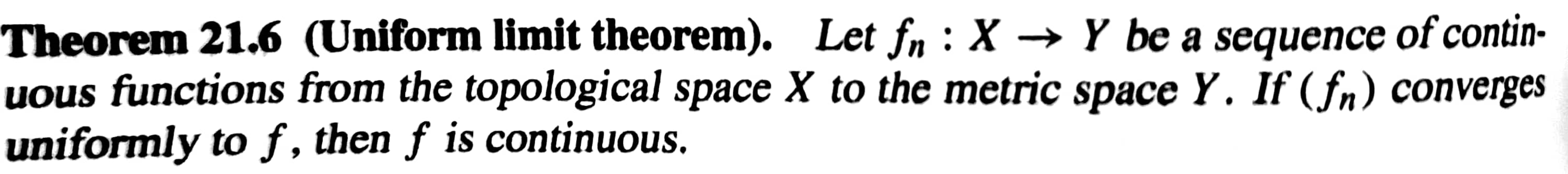
Uniformly converges는 f가 continous하다는 것을 보일 때 이용될 수 있다. (단, Y가 metric topology이어야 함.)

증명은 위와 같다!
핵심은 triangle inequality를 사용하는 것!
[Topology 정리4]: https://kyujinpy.tistory.com/120
마지막은 topology의 꽃인 Connectedness와 Compactness에 대해서 살펴봅시다!
References by https://product.kyobobook.co.kr/detail/S000003154978
Topology | James Munkres - 교보문고
Topology | For a senior undergraduate or first year graduate-level course in Introduction to Topology. Appropriate for a one-semester course on both general and algebraic topology or separate courses treating each topic separately. This text is designed to
product.kyobobook.co.kr
'MATH > Topology' 카테고리의 다른 글
| [Topology 정리2] - Closed, Closure and Hausdorff (2) | 2023.12.24 |
|---|---|
| [Topology 정리1] - Open, basis and topology spaces (1) | 2023.12.19 |

