*Topology (위상수학)에 대해서 정리한 글입니다.
*두서가 없을 수도 있고, 위상수학을 복습한다는 마음으로 정리했습니다!
*입문하시는 분들께 도움이 되었으면..ㅎㅎ
Contents
- Topology with open
- Finer and coarser
- Basis 정의
- Topologist on R
- Order topology
- Product topology
- Subspace topology
Introduction

위의 이미지는 위상수학하면 떠오르는 가장 대표적인 예시가 아닐까 싶다.
Cup과 도넛은 왜 위상적으로 같은가?
아마 많은 사람들은 '구멍이 1개이기 때문입니다`라는 답을 할 것이다.
아주 명확하게 맞는 말이다!
그렇다면 어떻게 수학적으로 증명할까? 2개의 공간이 동형이라는 말은 어떤 조건이 필요할까?
위의 증명을 거리개념으로 표현할 수 있는가?
이러한 의문점이 든다면, 위상수학을 꼭 배우길 추천한다.
위상수학은 우리가 살아가는 여러 space에 대한 표현들을 거리개념 없이, 단순히 open과 close로 모든 걸 설명한다.
거리개념없이 연속성 및 극한 증명, 2개의 사상이 동형인지 증명하는 것은 매우 흥미롭다. 한번 살펴보자!
Open의 위상적 정의
Topology with open

위는 topological space T에 대한 정의이다.
간단히 말하면,
1) 공집합과 X를 포함하고 있어야 한다.
2) 무한한 union subset에 대한 subcollection은 T에 속하고,
3) 유한한 intersection subset에 대한 subcollection은 T에 속한다.
*추가적으로 the subset A of X는 open set이다.
2), 3)번에 대해서 의문점이 들 수도 있다.
일단 2)번은 trivial하다. (3)번은 무한한 intersection subset이면 무조건 open set이 아닐 수도 있다.
예를 들어 (-1/n, 1/n)이라는 open ball이 실수집합 안에 정의되어 있다고 가정해보자.
1) 정수집합에 속한 n에 대하여 무한한 intersection subset을 한다면, {0}이 나올 것이다.
2) 이때, R-0은 open set이다. 즉, {0}은 closed set이다.
(*추후에 다뤄질 내용; open과 close는 서로 반대의 개념; 물론 open이면서 close일 수도 있음)
Finer and Coarser
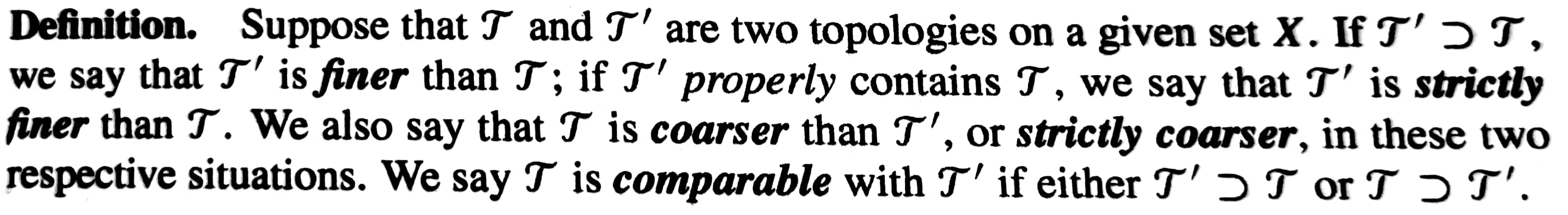
Finer and Coarser는 topology space 간의 비교를 할 때 이용되는 개념이다.
T의 basis가 T`의 basis안에 들어갈 수 있으면,
T`은 T보다 coarse한 것이고, T는 T`보다 finer 한 것이다.
(*Topology with basis에 대한 개념은 아래에서 설명)
이것을 통해서 실수 집합 안에서 정의되는 여러 topology spaces간의 비교를 할 수 있다.
밑에 basis까지 다 설명하고 1~2개 정도 example를 소개해보겠습니다.
Basis 정의

Basis 정의는 위와 같다. Topology에서 정의되는 basis는 collection의 개념으로 보면 좋다. 즉, basis elements이다.
간단히 말하면,
1) X안에 속하는 x element에 대하여 최소 한개 이상의 basis에서 x를 포함하고 있어야 한다.
2) Basis A와 B가 있을 때, basis collection안에 들어있는 임의의 basis C는 A와 B의 교집합에 속한다.
Topology basis는 너무 중요한 개념이다. Topology space를 만들거나 비교할 때, topology space에 속하는 모든 open set들을 모두 고려해야했다.
그러나 basis는 `topology T generate by basis B`라는 중요한 특성이 있기 때문에, basis B만 찾는다면 매우 수월해진다.
이러한 관점에서, 2번의 정의가 매우 중요하다고 할 수 있다.
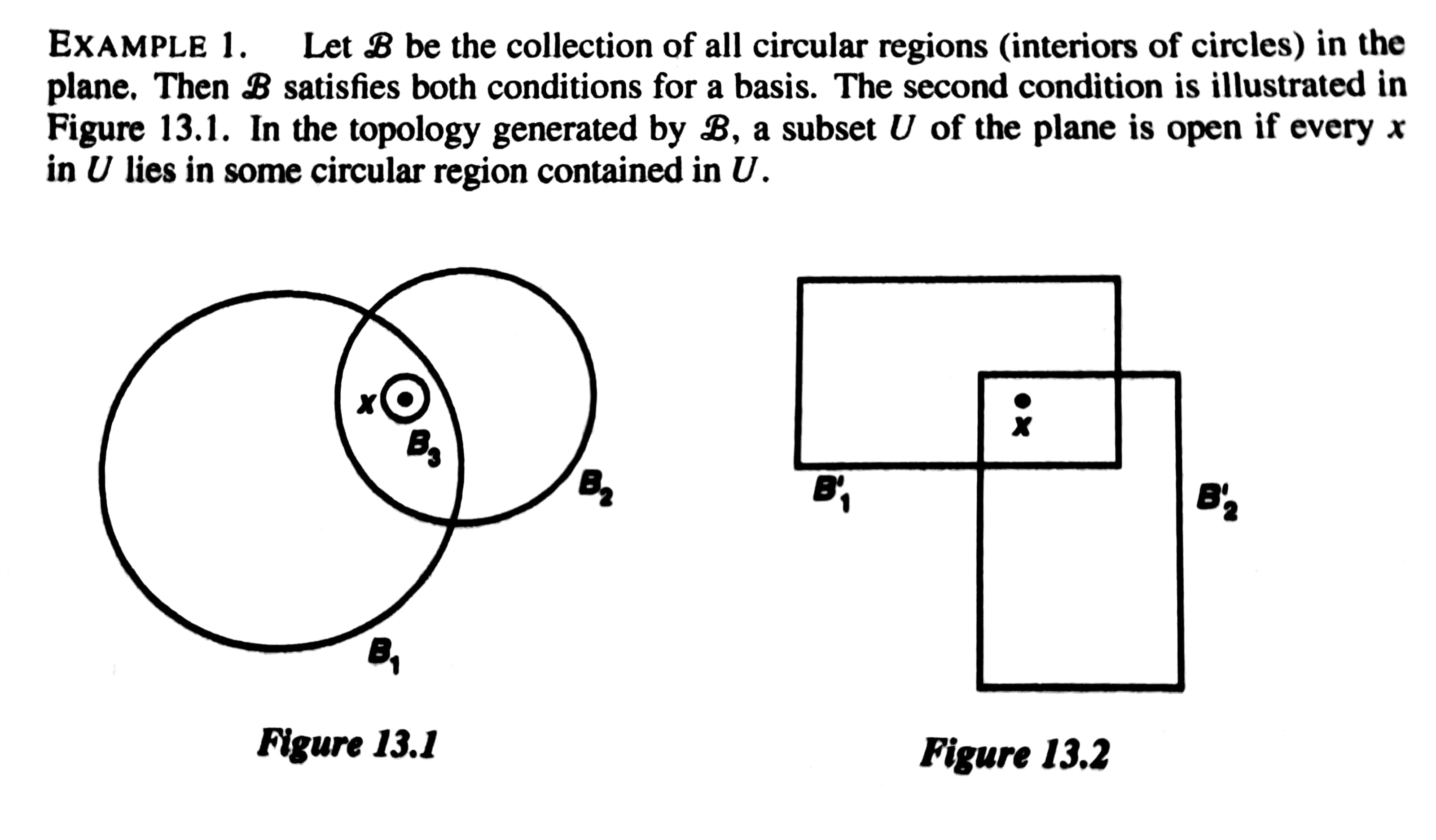
위의 그림을 본다면 더욱 이해가 쉬울 수도 있다!
특히 13.1이 (2)번에 대한 개념을 명확히 설명하고 있다.

Basis의 재미있는 특징으로, the collection of B의 모든 union은 topology T이다. (Trivial 함!)
Topologist on R

Basis를 활용해서 어떻게 비교하는지 살펴보면,
1) T`가 T보다 finer할 때,
2) T`의 basis B`는 T의 basis B안에 속한다.
쉽게 이해하면, B`이 B를 표현할 수 있다는 것이다. 이 말은 T`안에 있는 basis로 T를 표현할 수 있기 때문에 T`이 finer하다는 의미가 된다.
위의 사실을 바탕으로 재미있는 example를 하나 풀어보자!

Space R에 대하여 2가지 basis로 정의된 topologies를 만들 수 있다.
1) Open ball basis, called B, T
2) Open square basis, called B`, T`
놀라운 사실은, 서로 다른 basis 만든 topologies T와 T`가 같다는 것일까? 왜 그럴까?!
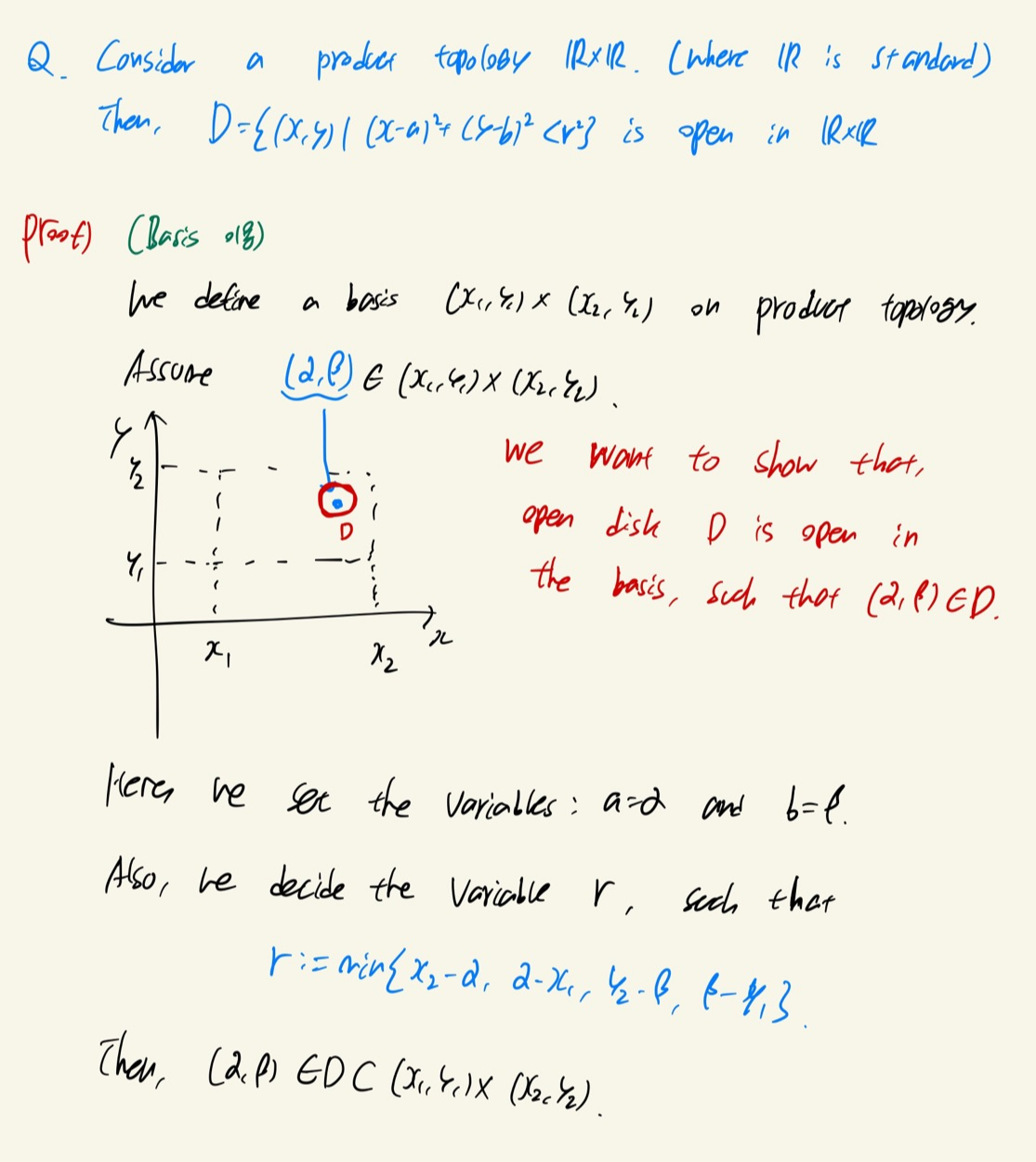
Open ball basis가 square basis 안에 들어갈 수 있다는 증명만 보였다.
반대쪽도 시도해보신다면(?) 마찬가지로 성립되며, 이로써 두 개의 topology는 서로 같다는 증명을 할 수 있다.

추가적으로, space R에 대하여 여러 topology가 있다.
각각 topology를 서로 비교해보고, 어떤 관계가 있는지 연습삼아서 풀어보면 도움이 될 것 같다!
Topologies
Order topology

Order topology는 topology space안에 `순서`가 있는 것이다.
1) (a,b)라는 임의의 open interval를 X안에서 잡을 수 있어야 한다.
2) a0라는 smallest element와 b0라는 larges element가 존재해야한다.
(*추가적으로 space R은 trivial하게 order를 가지고 있음)
Order topology를 통해서 discrete topology도 체크할 수 있다. (아래 하나의 example 증명)
(*discrete topology는 하나의 원소가 open set인 space이다.)

Product topology

Product topology는 앞으로도 굉장히 많이 이용될 예정이다.
Basis도 간단하게 각각의 basis의 product로 표현가능하다.
Subspace topology

Subspace topology는 위와 같이 정의된다.
1) X의 subset Y가 있다고 한다면, topology에 속하는 U와의 intersection을 이룬 것의 collection이 subspace topology이다.
2) 여기서 U는 X의 open set이다.
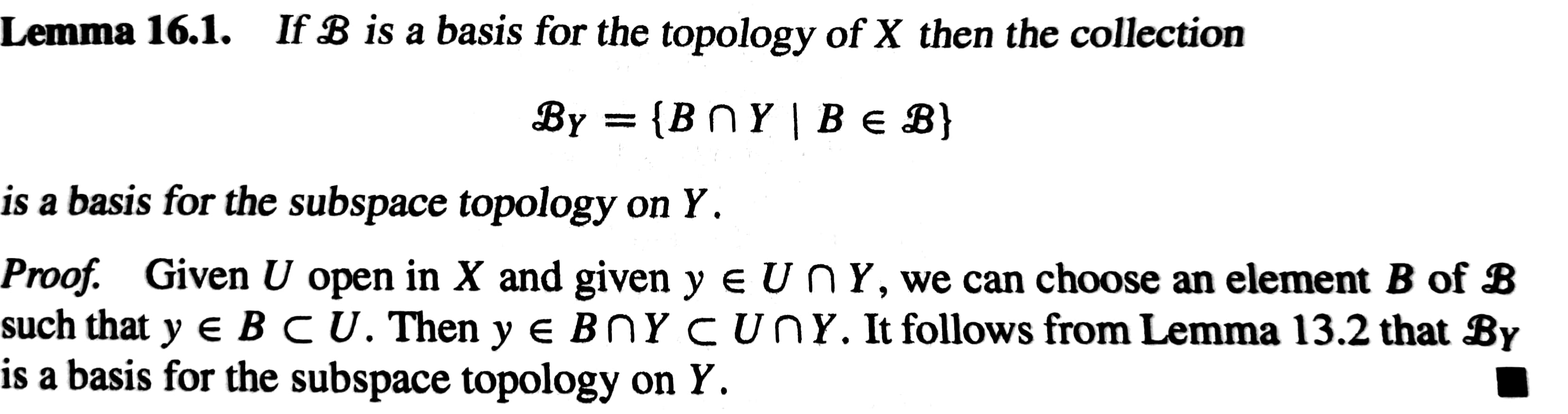
Subspace의 basis는, X의 basis와 Y간의 intersection으로 구성된다!
Topology 정리2: https://kyujinpy.tistory.com/116
[Topology 정리2] - Closed, Closure and Hausdorff
kyujinpy.tistory.com
다음 글에서는, closed와 hausdorff space에 대해서 살펴보겠습니다!
References by https://product.kyobobook.co.kr/detail/S000003154978
Topology | James Munkres - 교보문고
Topology | For a senior undergraduate or first year graduate-level course in Introduction to Topology. Appropriate for a one-semester course on both general and algebraic topology or separate courses treating each topic separately. This text is designed to
product.kyobobook.co.kr
'MATH > Topology' 카테고리의 다른 글
| [Topology 정리3] - Continuous and metric topology (1) | 2023.12.24 |
|---|---|
| [Topology 정리2] - Closed, Closure and Hausdorff (2) | 2023.12.24 |

