*VAE 수학적 지식을 리뷰하기 글입니다! 궁금하신 점은 댓글로 남겨주세요!
*(통계학, 확률론 지식이 있다고 가정합니다.)
VAE paper: https://arxiv.org/pdf/1312.6114.pdf
Contents
Simple Introduction
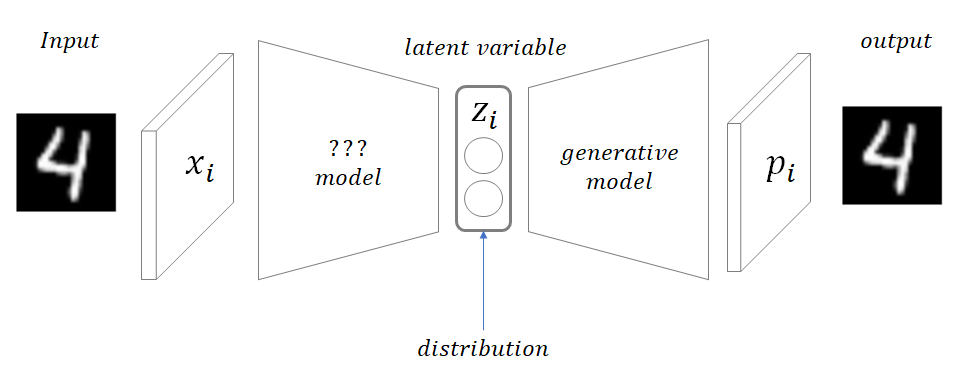
VAE는 컴퓨터 비전 분야에 한 획을 그은 방법론이다.
특히 image generation 분야에서는 엄청나다고 할 수 있다.
요즘은 VAE보다 훨씬 진보된 모델 diffusion이 자리를 아예 잡고 있어서 해당 논문을 이해하지 않는다면 최신 트렌드를 따라갈 수가 없다.
Diffsion을 예전에 공부했었는데 기억이 가물하고, Diffusion을 이해하기 위한 초석이 바로 VAE에 나오는 수학적 이론이기 때문에 VAE부터 제대로 공부하고자 한다!!
Method
Intractable
해당 논문의 초입부에는 두개의 확률분포를 추정하는데 있어서 어떠한 어려움이 있는지 얘기해주고 있다.

일단 가정부터 살펴보자.
연속적인 또는 이산적인 독립변수 x를 N개 가지고 있는 Dataset X를 정의하자.
이때 data는 관찰되지 않은 랜덤한 연속변수 z에 의해서 생성된다고 하자!!
그렇다면 해당 process는 2단계로 이루어질 수 있다.
1. 랜덤변수 z는 사전분포 P_θ(z)에 의해서 생성된다.
2. data x는 조건분포 P_θ(x|z)에 의해 생성된다.
(추가적으로 해당 함수들은 미분가능하다고 가정한다.)

그러나 논문의 필자들은 위의 분포들을 계산하는 것이 기존의 방법으로는 매우 다루기 어렵다고 한다.
첫번째로 marginal likelihood의 수식을 보면 알 수 있다.
당연히 data X가 P_θ function으로부터 나와야 하지만, 해당 수식은 정의되지 않은 분포 z를 이용하기 때문에 추정하기 매우 어렵다. (그렇기 때문에 MAP(maximum a posteriori), ML(maximum likelihood)을 이용하기 힘들다.)
두번째로는 large dataset 문제이다.
그렇기 때문에 sampling을 기반으로 하는 Monte Carlo EM 등등은 매우 속도가 느릴 수 밖에 없다.
그렇다면 해당 문제를 어떻게 풀어야 할까!?
Variation lower bound

시작에 앞서서 해당 글을 읽으면 구조에 어느정도 도움이 될 수 있다.
여기서는 recognition model q_φ(z|x)와 다루기 힘든 true posterior p_θ(z|x)로 구분한다.
또한 해당 논문에서는 parameter φ를 θ와 같이 학습하는 방법론을 소개한다.
코딩 base에서는 recognition model이 encoder, posterior가 decoder이다.

한번 이 식을 뜯고 맛 볼 것이다.
먼저 일단, marginal likelihood를 각각의 data point마다 계산한다.
(*marginalization한다는 것은 가능한 주변 확률의 경우의 수를 모두 고려한다는 것이다. 즉 marginal likelihood(주변 우도)는 주변 모수들을 모두 고려한 우도를 계산한다는 것이다.)
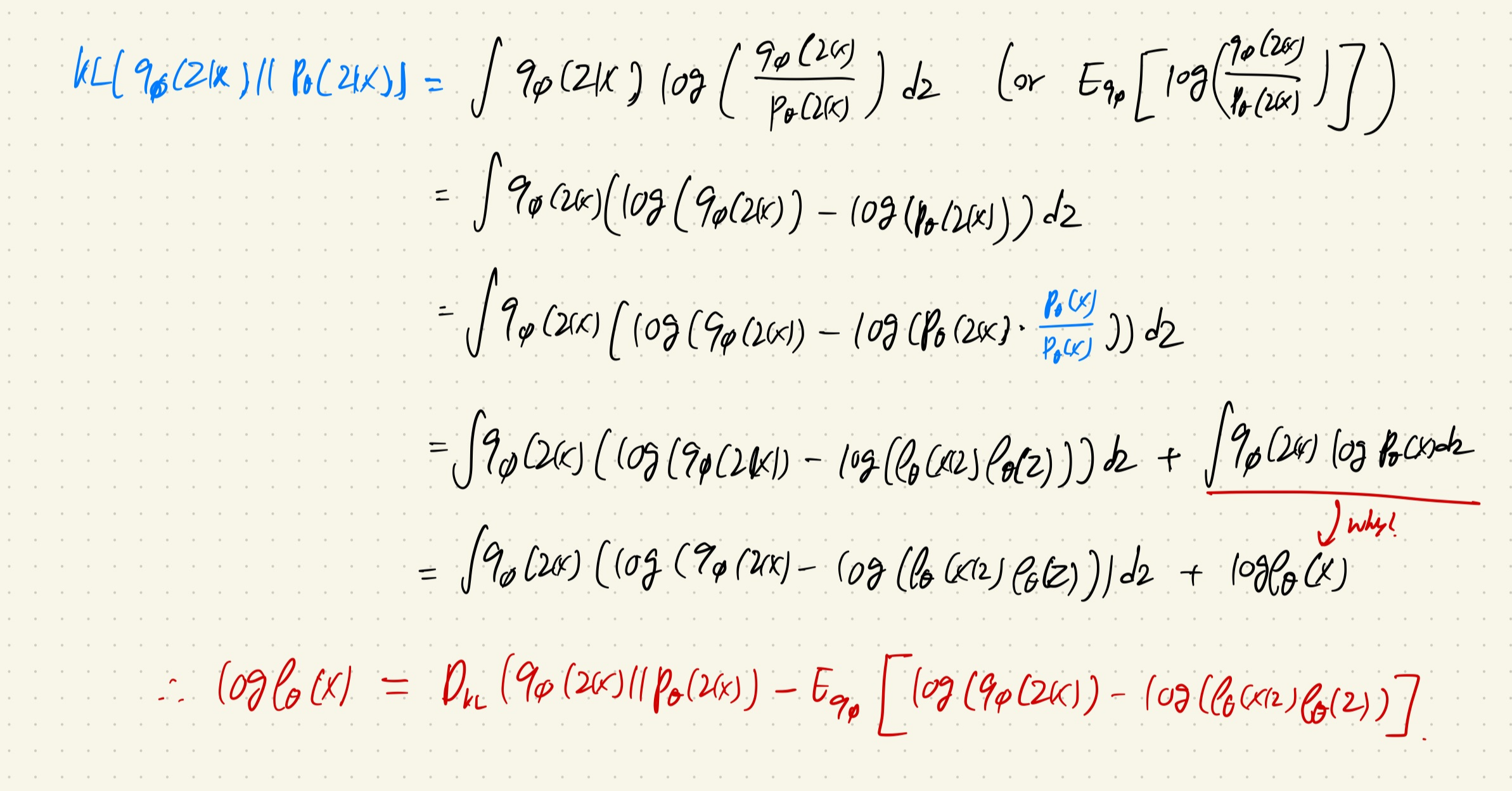
이제 Equation 2를 한번 풀어보겠다.
KL-divergence 수식을 역으로 이용하여서 위의 사진 처럼 전개를 하면 log(p_θ(x))가 나오게 된다.
이를 정리하면 맨 아래와 같은 식이 만들어 진다.
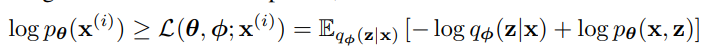
여기서 마지막항은 ELBO라고 할 수 있다.
(논문에서는 second RHS term이라고 하기도 한다.)

ELBO를 깔끔하게 정리하면, KL-divergence와 사후분포에 대한 기댓값에 대한 식으로 바뀌게 된다.
여기서 second RHS term은 variation lower bound가 된다.
여기서 KL-Divergence를 직접 구하는 것은 힘들기 때문에 사후분포에 대한 값을 maximize해서 latent variable z로 부터 x가 나올 기댓값을 크게 만든다.
여기서 KL-divergence는 regularization 역할을 하는 term으로 두 분포가 유사해지도록 하는 역할을 한다.
즉, variation lower bound를 최대화하는 방향으로 optimization을 수행한다.
+) VAE loss function은 보통 위의 second RHS term(ELBO)에 음수를 곱한 값으로 이용한다!
Reparametrization trick

Lower bound를 최대화하는 방식으로 학습이 이루어지기 위해서 backpropation을 수행해보자.
이때, lower bound을 계산할 때 z는 sampling되어서 추출되므로 parameter φ는 backpropagation이 진행되지 않는다.
이걸 해결하기 위한 것이 바로 Reparametrization trick이다.

기존의 q_φ가 backpropagation이 되지 않았으므로, 미분가능한 변환함수 g_φ(ε, x)을 새롭게 정의한다.
여기서 ε은 noise variable이다.
그렇다면 새롭게 정의되는 latent variable z는 g_φ(ε, x)라고 할 수 있다. (equation 4)

이제 위에 정의된 differentiable transformation functino을 가지고 Monte Carlo estimates of expectations을 이용하여 q_φ에서 f(z)에 대한 기댓값을 계산한다. (Lower bound의 두번째 항)
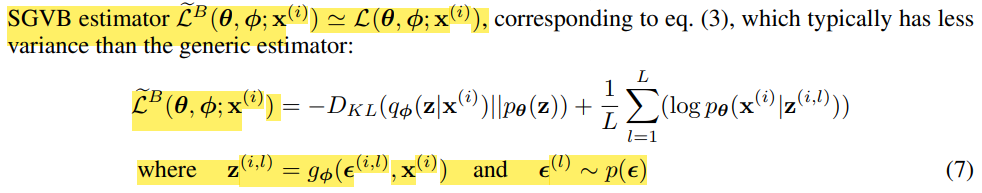
그리고 SGVB(stochasitc gradient variation bayes)에서 lower bound를 구하면 equation 7과 같은 모습이 된다.
(equation 5을 대입한 것.)
자 이제 reparametrization trick을 설명하기 위한 용어 및 수식 정리는 끝났다!

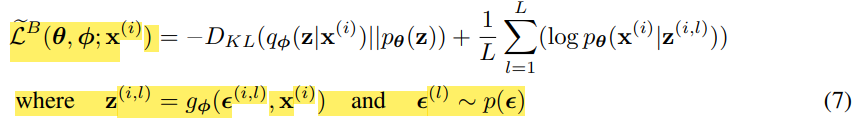
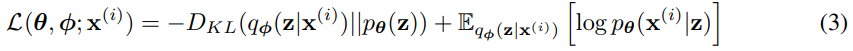
Equation 7과 3을 비교해보면 왜 backpropagation이 가능해졌는지 알 수 있다.
1. Equation 3은 z가 sampling을 하기 때문에 사칙연산 등등에 대해서 gradient 계산을 못한다. 즉 model 자체에 stochasitc이다.
2. Equation 7은 transformation function인 g_φ(ε, x), where ε ~ p(ε)을 이용해서 p(ε)이 stochasitc하고 z는 gradient하도록 변했다.
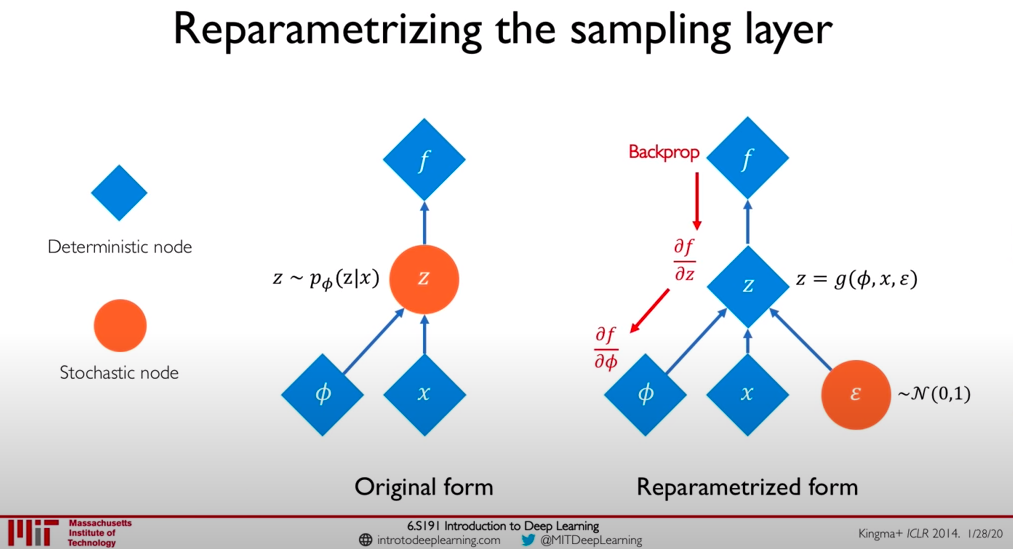
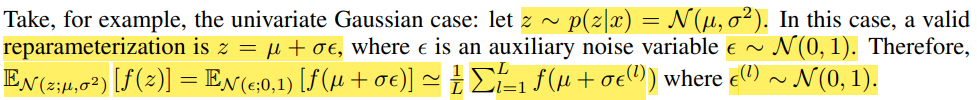
위의 예시를 한번 읽어보면서 상기하면 이해가 될 것이다(?)
*몇 줄 요약: 기존의 q_φ(z|x)에서 sampling 되던 z는 gradient 계산이 안되기 때문에 parameters φ, x, ε ~ p(ε)을 이용해서 differentiable transformation function g_φ(ε, x)을 만들어서 z = g_φ(ε, x)의 수식을 만들면 z는 gradient 연산이 가능하기 때문에 기존의 우리가 찾고자 하던 q_φ(z|x)을 이용하지 않더라도 φ에 대해서 학습할 수 있다.

+) 논문의 저자들이 어떤 differentiable transformation function과 noise variable을 골라야 하는지에 대한 가이드라인(?)을 적어두었다.
References
첫번째 이미지 references: https://taeu.github.io/paper/deeplearning-paper-vae/
- 2023.07.09 Kyujinpy 작성.
'MATH > Statistics' 카테고리의 다른 글
| Markov chain(마르코프 연쇄; markov process) (0) | 2023.07.08 |
|---|
